Frequencies of levels of a categorical variable
When we encountered categorical variables in two sample t-tests or ANOVA they were the treatment groups we wanted to compare - for example, the heart rates of lobsters were compared between GABA-treated and control groups, which we represented as a variable "Treatment" with levels "GABA" and "Control. In a t-test or ANOVA the categorical variable is a predictor variables - it is the variable we experimentally set, so that we can measure another variable (such as heart rate) as a response.
However, it is possible for response variables to be categorical as well. We summarize categorical variables by counting up frequencies of occurrence of each level, which gives us a set of counts that we can analyze.
Today we will focus here on frequencies of just a single categorical variable at a time, and we will ask how the distribution of frequencies compares with some hypothetical sets of frequencies of interest. In this sense the question we'll ask is like a one-sample t-test, in which we hypothesized a population mean (such as body temperature of 98.6 degrees) and then compared the mean of some data on body temperatures to the hypothetical population value. With categorical frequencies we will need to specify a different hypothetical value for each categorical level.
Imagine you are interested in studying the distribution of head injuries in high school athletes participating in various sports in the United States. Data showing the number of concussions are in the table below.
| Sport | Concussions |
|---|---|
| Basketball | 9,572 |
| Football | 62,353 |
| Lacrosse | 3,508 |
| Soccer | 22,955 |
| Baseball | 2,579 |
It is clear from this table that football players get the most concussions by far, and baseball players get the fewest. It seems that football is the most dangerous and baseball is the least dangerous sport based on these numbers. But, is it valid to draw a conclusion by just comparing the numbers of concussions between the sports?
The problem with direct comparisons like this is that it's likely that a different number of students participate in each sport. It's possible that more students participate in football than other sports, in which case we would expect more concussions for football players, even if the chances of a concussion are the same on a per-student basis.
To make a more reasonable assessment, we need a baseline that gives an idea of how many concussions to expect if all of the sports are equally dangerous. One way to do this is to use data on number of participants - if sports are all equally dangerous then we would expect concussions to be in proportion to the number of participants.
| Sport | Concussions | Students participating |
|---|---|---|
| Basketball | 9,572 | 76,015 |
| Football | 62,353 | 103,921 |
| Lacrosse | 3,508 | 13,396 |
| Soccer | 22,955 | 89,798 |
| Baseball | 2,579 | 42,977 |
| Totals | 100,967 | 326,107 |
You'll see now that the numbers of concussions could very easily be influenced by the number of students participating in each sport, because the numbers of participants vary greatly. Football does indeed have the most participants, and the two seemingly safe sports (lacrosse and baseball) have fewer.
So, at least some of the variation in concussions seems to be due to differences in participation rates. However, we don't expect the number of concussions to equal the number of participants, because the totals are different. First, we need to calculate the number of concussions we would expect given the numbers of students participating in each sport.
| Sport | Concussions | Proportion of students participating |
|---|---|---|
| Basketball | 9,572 | (76,015/326,107 =) 0.233 |
| Football | 62,353 | (103,921/326,107 =) 0.319 |
| Lacrosse | 3,508 | (13,396/326,107 =) 0.041 |
| Soccer | 22,955 | (89,798/326,107 =) 0.275 |
| Baseball | 2,579 | (42,977/326,107 =) 0.132 |
| Totals | 100,967 | 1 |
The first step in calculating the expected frequencies of concussions is to convert the frequencies of participants to relative frequencies. If you recall, relative frequencies are proportions of the total number of observations. The relative frequencies for each sport are shown to the left (Proportion of students participating), which are calculate by dividing the number of participants in each sport by the total participants.
These proportions tell us the rate at which we would expect concussions to occur, if each sport is equally dangerous and concussions are in proportion to participation. In other words, if all the sports were equally dangerous we would expect 23.3% of concussions to occur in basketball players, 31.9% to occur in football players, etc.
| Sport | Concussions | Proportion of students participating |
Expected number of concussions |
|---|---|---|---|
| Basketball | 9,572 | 0.233 | (0.233 x 100,967 = ) 23,525.3 |
| Football | 62,353 | 0.319 | (0.319 x 100,967 = ) 32,208.5 |
| Lacrosse | 3,508 | 0.041 | (0.041 x 100,967 = ) 4,139.6 |
| Soccer | 22,955 | 0.275 | (0.275 x 100,967 = ) 27,765.9 |
| Baseball | 2,579 | 0.132 | (0.132 x 100,967 = ) 13,327.7 |
| Totals | 100,967 | 1 | 100,967 |
Now we can calculate the expected frequency of concussions by multiplying the total number of concussions (100,967) by the proportion of students participating in each sport. For example, since 23.3% of the 100,967 concussions are expected to occur in basketball players, the expected frequency is 0.233 x 100,967 = 23,525.3. Expected frequencies for all of the sports are shown in boldface, with the calculations in gray.
You'll see that the total is the same for the observed number of concussions and for the expected number of concussions, so now we have numbers that we can appropriately compare against each other.
The frequency of concussions and their expected frequencies are shown below, with observed numbers of concussions in blue, and the expected number in red. It certainly looks like football is more dangerous than the other sports, as it's the only sport in which the observed frequency is greater than expected.
The null hypothesis
But before we jump to conclusion we have to remember that these data are a sample from a population, and the frequencies are subject to random variation. We need to know these frequencies are affected by random variation to understand the null hypothesis we will use. The graph to the left will simulate the frequencies of concussions that we would expect if concussions were proportional to participation rates, subject to random sampling.
If you push the "randomize" button a new set of 100,967 concussions are selected, with the probability of occurring in each type of sport being equal to the proportion of students participating.
The first thing you'll see is the obvious change from observed frequencies - the new "observed" numbers that you generated at random match very closely to the expected numbers of concussions. But, there are slight differences still between observed and expected numbers due to random sampling. If you click the "Randomize" button repeatedly (and watch the bar heights closely) you'll see that the blue bars change very slightly each time as a new "observed" sample is selected. Note also that the red expected numbers are always the same, because each randomization uses the same total number of concussions.
Random distributions of concussions in proportion to the frequency of participants is a null hypothesis for these data. Null hypotheses are always hypotheses of no effect - if there is no effect of being in one sport or another, then the frequency of concussions should be in proportion to the frequency of participants. To evaluate the chances that the distribution of concussions is just a random sample from a population in which all of the sports are equally dangerous, we need a way to quantify how much difference there is between the set of observed frequencies and the set of expected frequencies, and then calculate a probability of the observed difference occurring by random chance.
The statistical test we will use to evaluate this null hypothesis is called a Chi-square goodness of fit test.
Chi-square goodness of fit tests
Chi-square goodness of fit tests are used to compare the match between observed frequencies and values expected given some process that is hypothesized to be producing them. We can express our null hypothesis that our observed data are in proportion to expected frequencies symbolically as:
Ho: Observed = Expected
Although we don't have Greek letters to remind us, this is still a hypothesis about a population - we're hypothesizing that at the population level the distribution of concussions is equal to the expected rates. If the null hypothesis is true, any difference between observed and expected is just due to random sampling variation.
To test a null hypothesis, we need a) an observed test statistic calculated from our data, and b) a sampling distribution that tells us what a large number of randomly generated test statistics would look like if the null hypothesis is true.
Test statistic
We will use the Pearson Chi-square test statistic to measure the amount of difference between observed and expected numbers. The formula is:
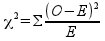
where O refers to the observed number of concussions for a sport, and E refers to the expected number. The (O-E)2/E quantity is calculated for each sport, then summed (Σ) across sports to give us our observed chi-square value. The standard symbol for a Chi-squared test statistic is lower case Greek chi (χ) squared.
If you look at the formula, it should be clear that the statistic is measuring the amount of difference between observed and expected frequencies. You can tell this from the formula if you notice:
- If there is an exact match between the observed data and the expected values, then all of the O-E differences will be 0, and the Chi-square statistic will be 0. Since expected values have to be positive, and squared differences have to be positive, negative values aren't possible, and 0 is the smallest possible value for χ2.
- As the observed frequencies diverge from expected values, the O-E's get bigger, and the Chi-square statistic will increase in size.
- The squared differences are being divided by expected values - this means that the amount of difference between observed and expected is relative to the expected numbers. Thus, the Chi-square statistic measures relative amounts of difference between observed and expected, not absolute amounts of difference.
We calculate the chi-square value for the concussion data like so:
| Sport | Concussions | Expected number of concussions | (O-E)2/E |
|---|---|---|---|
| Basketball | 9,572 | 23,535.3 | 8,276 |
| Football | 62,353 | 32,208.5 | 28,212 |
| Lacrosse | 3,508 | 4,139.6 | 96 |
| Soccer | 22,955 | 27,765.9 | 833 |
| Baseball | 2,579 | 13,327.7 | 8669 |
| Totals | 100,967 | 100,697 | χ2 = 46,086 |
The sum of the (O-E)2/E values is shown in bold italics, and this is our observed Chi-square test statistic.
Sampling distribution
Now we need a sampling distribution to compare this test statistic to so that we can obtain a p-value. Remember, sampling distributions are probability distributions that mathematically model randomly sampling from a population. In this case, the random sampling we are modeling is illustrated in the graph above when you hit the "Randomize" button - the random samples assume that the null is true, and that concussions are in proportion to participation rates, but random chance makes the observed frequencies differ somewhat from these expected proportions. If we calculated a Chi-square statistic for each of the random samples generated, the distribution of these statistics would follow a Chi-square distribution. We can thus use the Chi-square probability distribution as a mathematical model of random sampling for our null hypothesis test.
A Chi-square distribution is shown in the graph below, with the rejection region for a Chi-square GOF test shaded red - just like with the other tests we've learned we use an alpha level of 0.05, so the area under the curve in the rejection region is 0.05. Since the Chi-square statistic uses squared differences it will always be positive, and since we are interested in whether deviations are large enough to be considered non-random we are only interested in the upper end of the curve. The critical value is the lower end of the rejection region, and is reported below the degrees of freedom setting.
Enter d.f. (categories - 1):
Critical value = 9.488
The shape of a Chi-square distribution depends on degrees of freedom. We are comparing observed to expected frequencies for five sports, so degrees of freedom is related to the number of sports, not the number of athletes. In a Chi-square goodness of fit test degrees of freedom equals the number of categories - 1. We have five sports, so there 5 - 1 = 4 degrees of freedom for these data.
The graph to the left is set initially to 4 degrees of freedom so you can see the distribution we will use for this analysis of concussion rates. The critical value for 4 degrees of freedom is Chi-square = 9.488, so we would reject the null with any Chi-square value greater than that.
You can change the degrees of freedom for the graph so you can see how the shape of the Chi-square distribution and location of the critical value changes. If you increase degrees of freedom the curve shifts to the right (note that the x-axis scale changes to keep the curve on the graph). This shift right reflects the fact that we're summing squared differences across categories, and with each additional categories there is an additional squared difference to add to the Chi-square statistic. Small differences become very unlikely as the number of categories increases, and a perfect match (Chi-square = 0) has a probability of 0.
Decreasing degrees of freedom shifts the curve back to the left, because small numbers of categories provide few opportunities for differences to accumulate. If you set degrees of freedom to 1 you'll see that large differences become very unlikely, and small differences are so common that the curve becomes asymptotic with the y-axis. This means that at 1 df the most probable amount of random difference is 0, with differences quickly becoming less probable as they increase in size.
At df = 2 the curve isn't an asymptote, but it increases at low numbers until it intersects the y-axis at p = 0.5.
At df = 3 or above the curve goes through the origin (0,0) and becomes a right-skewed curve with a single mode near a χ2 value of 1, meaning that differences of 0 become impossible, and Chi-square values of around 1 become the most likely.
p-value
Now that we have the correct Chi-square distribution identified we can calculate a p-value. The observed chi-square statistic is 46,086, and the area under the Chi-square distribution with 4 degrees of freedom from 46,086 to infinity is...tiny. If we use MINITAB or Excel to do the calculation we will get a p-value like 1 x 10-16, which is the smallest decimal number that it can produce. Based on this p-value we would reject the null, and conclude that the observed data aren't equal to expected, and therefore concussions are not in proportion to participation rates.
We now have reason to think that some sports are more dangerous than
others, but the null hypothesis is about a match between observed and
expected frequencies collectively, and rejecting the hypothesis doesn't
tell us which sports produce significantly more or less concussions than
expected. We will address that question next.
Which sport is most dangerous?
We can get an idea of which sport is most dangerous just by comparing the observed and expected values - football is the only sport in this set that has more concussions than expected. However, comparing the amount of difference between observed and expected values between the sports is complicated by the fact that the expected numbers are really different among the sports. Lacrosse has an expected value of 4139.6 concussions, so it isn't possible for lacrosse to be under its expected value by more than 4139.6. Both baseball and basketball are below their expected values by more than this, but there are many more students that participate in these sports, and they have much higher expected values to begin with. If we wanted to know whether lacrosse was more or less safe than baseball or basketball we would need to account for the differences in numbers of participants.
We can correct for this difference in expected value by calculating standardized residuals that give us a relative amount of difference from expected that can be compared between the sports. We encountered residuals when we learned about regression analysis - residuals are differences between observed and predicted values. Standardizing means to convert the difference into standard deviation units, like a z-score. A standardized residual in a Chi-square GOF analysis is calculated as:
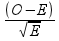
The structure is like the chi-square formula, but we are only calculating a value for one sport at a time, and instead of squaring the differences (which ensures we will always have positive chi-square values) we use the raw difference in the numerator and divide by the square root of the expected - standardized residuals thus have a sign that indicate whether the observed value was above (+) or below (-) expected. Standardized residuals are approximately normally distributed, so a standardized residual that exceeds -2 or 2 indicates an observed value that is significantly different from expected. The standardized residuals are here:
| Sport | Concussions | Expected number of concussions | Std. Resid. |
|---|---|---|---|
| Basketball | 9,572 | 23,535.3 | -91 |
| Football | 62,353 | 32,208.5 | 168 |
| Lacrosse | 3,508 | 4,139.6 | -10 |
| Soccer | 22,955 | 27,765.9 | -29 |
| Baseball | 2,579 | 13,327.7 | -93 |
| Totals | 100,967 | 100,697 |
All of the standardized residuals are below -2 or above 2, so all would be considered significantly different from expected. Football is by far the sport most likely to lead to a concussion - the observed number of concussions is 168 standard deviations above the expected value. The least likely to produce a concussion is baseball (it has the negative standardized residual with the biggest absolute value), but basketball is only 2 standard deviations closer to its expected value - only slightly more dangerous than baseball. Soccer is next, followed by lacrosse.
Effects of sample size on power of a Chi-square test
The number of data points isn't used explicitly anywhere in the Chi-square goodness of fit test. This is very different than the other tests we used, in which degrees of freedom were based on the number of data points, and larger sample sizes had obvious effects on the power of the test. It might seem almost unfair to collect over 100,000 data points and still only have 4 degrees of freedom, but fear not - having a bigger sample size does in fact increase our power to detect differences from expected values.
We will see how this is true by revisiting the simulation of the null hypothesis we saw above, but this time we have the ability to set the sample size. As before, we can randomize the data at the sample size we select, and each time we will see the results of the Chi-square goodness of fit test.
Chi-square = , p =
Enter a total number of concussions
We will just work with randomly generated data this time - since the "observed" frequencies are being randomly generated assuming that concussion rates are the same for all sports, the null hypothesis is true in all of these simulations.
We can only be certain that our results show a real, non-random difference if it's bigger than the differences that chance can produce. Because of this, if our design allows for large differences to occur by chance, we would need even bigger differences in our observed data before we could conclude that there is a real, non-random difference. Which is to say, big chance differences mean lower statistical power, and small chance differences mean high statistical power.
To start, leave the sample size at the default and click on the "Randomize at this n" button several times. Note that about once every 20 times you click the button you get a p value less than 0.05, which is what we expect when the null hypothesis is true (the p-value will turn red when it is less than 0.05). But, also note that the relative differences between the bars are very small - each time you hit the "Randomize at this n" button a new set of random data is produced, but the heights of the bars are always very close together. Pay particularly close attention to the amount of difference you see when you do get a p < 0.05 - this is the amount of difference needed to reject the null, and the observed bars are still pretty close to the expected bars even when we reject the null.
Now, set the sample size to 1000. You will see that there are larger differences in the heights of the bars with each new random draw. You will still get about 1 in 20 p-values less than 0.05, but when you get them the amount of relative difference between the heights of the bars will be bigger than you saw at a sample size of 100,967. This means that you need a larger relative difference between observed and expected to reject the null at a sample size of 1000 than you needed at a sample size of 100,967.
Drop the sample size again to 100, and it will be even more clear that there are pretty big relative differences between observed and expected when p-values are less than 0.05. You need pretty big relative differences at a sample size of 100 to reject the null.
Hopefully you can see that at big sample sizes small relative differences between observed and expected can be statistically significant - the Chi-square test becomes more sensitive to small differences at big sample sizes, even though the degrees of freedom are the same for all sample sizes.
Assumptions
Chi-square goodness of fit tests are used on frequencies of categorical data, and do not have any assumptions about the distribution of the data. It is assumed that the data values are independent, and are from a random sample of the population. Independence in count data like this means that one athlete's concussion doesn't make it any more or less likely that any other athlete will get a concussion (as you'll see in the bees and hummingbirds as pollinators example we are sometimes interested in detection a violation of this assumption as a research question).
The Chi-square test statistic we use is more correctly called Pearson's Chi-square test statistic, and it only follows the Chi-square distribution at fairly large sample sizes. The problem is related to the fact that the expected values are continuous numbers, but the data are discrete counts. There will inevitably be some amount of mismatch between observed and expected because of this, which adds some error to the test.
The problem is small and can be ignored when sample sizes are big enough that the expected values are fairly large, but at small sample sizes the error can be quite large. For example, if we have an expected value of 0.1, the two closest counts possible are 0 and 1. If the count was 0, the contribution to the Chi-square statistic would be (0-0.1)2/0.1 = 0.1 - a very small addition to Chi-square. But, if the count was the second closest possible, the contribution becomes (1-0.1)2/0.1 = 8.1 - a much bigger addition to Chi-square for a small amount of difference.
To avoid problems with mismatches between the variable type for the data and for the expected values, the Pearson Chi-square statistic should only be used if:
- No expected values are below 1
- No more than 20% of expected values are less than 5
With 5 categories, only 1 could have an expected value less than 5 (but it would still need to be greater than 1).
Interpretation of results depends on the source of expected values
When we test for goodness of fit, we are assessing how well a model matches our data. The proportional model we've been working with so far says that there is a rate per observation that is the same for every category. In the concussion example, the concussion rate is the same for every student, regardless of the sport. If this is true, then the numbers of concussions should be proportional to the number of participants, because every sport is equally risky.
The basic framework for interpreting a goodness of fit test is the same, regardless of what model we use to produce expected frequencies:
- If we find a good match between observed frequencies and the expected frequencies produced by a model, we conclude that the data have the properties of the model - if concussions were in proportion to participation, we would conclude that every sport is equally risky.
- If the data don't match the model predictions, we conclude that the data do not have the properties of the model - we rejected the null, and found that football has a much greater chance of producing concussions than baseball.
However, there will be circumstances in which proportionality is not the correct model. We will look at a couple of examples in which we derive expected values from a theoretical distribution.
The binomial distribution
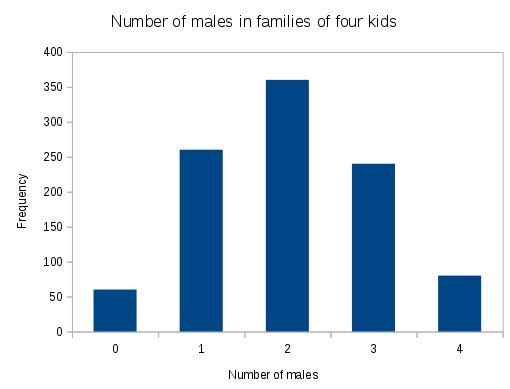
Imagine we found 1000 families of 4 kids, and counted up how many boys were in each of them. If we then counted up the frequencies of each number of boys we might get a distribution of frequencies like the one on the left. The x-axis gives the number of boys counted (which in a family of 4 could be 0, 1, 2, 3, or 4 boys), and the y-axis is the number of families that had each number of boys. We know some things about sex determination, and based on the fact that when sperm cells are formed there are an equal number of Y and X chromosomes available it's reasonable to think that the probability of having a boy is 1/2. We would expect based on this that two boys would be the most common number, which is what we see here. But, how many times would we expect 1 boy, or 3? Or 0 or 4? With a probability of 0.5 that each child will be a boy it seems that having 1 or 3 would be more likely than having 0 or 4, but how much more likely? In addition to needing a way to predict how many families would have each of the possible number of boys, we also could be wrong in our expectation that the probability of each child being a boy is 0.5 is wrong - certainly, the overall proportion of boys may be different from 1/2 if Y sperm are either better or worse at fertilizing eggs. Or, it could be that boys have higher or lower survival rates than girls. |
We need something other than the proportional model for data like these, and the binomial probability distribution is a much better choice. The binomial distribution allows us take what we know about the probability of a "success" on a single "trial" and predict the probability of obtaining x successes out of k trials.
For example, if we want to know the probability of x males (successes) in a family of 4 kids (trials) given that the probability of a male is 1/2, we can calculate this probability using the binomial distribution.
The formula for calculating binomial probabilities looks complicated, but is actually relatively simple:
![]()
In this equation, k is the number of trials - k is the family size for our data, which is 4. The number of "successes" is x - in our example x is the number of male births (note: "trials" and "successes" are traditional terminology for the binomial distribution, and are not meant to imply that male births are "successes" and female births are "failures"). The probability of a male child for each birth is p - in our example, we set p to 0.5. The probability of a female birth is 1-p, and k-x is the number of females in the family. We need to include (1-p) and k-x because in order to have (for example) two males out of four births we also have to have two females.
We are expecting that 2 males out of 4 births will be the most common when p = 0.5, and according to the binomial distribution the probability of 2 boys out of 4 kids is:
![]()
which you can confirm for yourself equals 0.38.
You can think of this formula as being made up of two parts. The part on the right, with the probabilities raised to exponents, gives the probability of a single family of four having two boys and two girls. This outcome can occur in many different ways (you can have a boy and a boy and a girl and a girl, or a boy and a girl and a boy and a girl, etc.), and to get the overall probability of getting two boys and two girls, we have to add up all the different ways this family composition can occur. The part on the left, with the factorials, calculates the number of different ways to get two boys in a family of four. The product of the two, then, gives the overall probability of getting two boys in a family of four.
Enter a probability of a boy
Enter a family size
If you do this probability calculation once for each number of males from 0 to 4, you get probabilities as shown in the graph to the left.
The initial graph uses a probability of p = 0.5, and it shows a symmetrical distribution of probabilities around 2.
We will continue to use p = 0.5 for this example, but this actually isn't quite correct, especially as we age. Men have shorter life expectancies than women, such that in the U.S. there are only 82 males per 100 female for people between 65 and 69 years old. This is equal to a probability of male of p = 82/(82+100) = 0.45. Think of this as being the probability of randomly selecting a single person between 65 and 69 years old who is a male. You can see how this value of p affects the shape of the distribution.
Between the ages of 95 and 99 there are only 26 males per 100 females. This translates into a probability of p = 26/(26+100) = 0.206 - check how this value of p changes the distribution.
If you change the family size you'll see that as long as p is set to 0.5 you get a symmetrical distribution. Large numbers for family size make the distribution more bell-shaped, to the point of appearing nearly normal when the family size gets really large.
If you set the probability to 0.5 and the family size to 4 the graph will match the binomial probabilities used in the next step.
Multiplying the binomial probabilities by the total number of families counted converts them to expected numbers of families that would have 0, 1, 2, 3, or 4 boys.
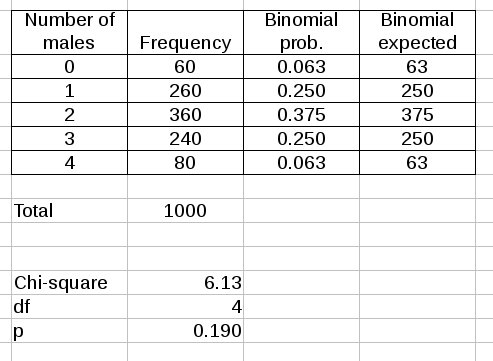 The
Frequency column are the counts of numbers of families with each number
of boys - it is the observed data. The binomial probabilities are
calculated using the binomial formula, and are the same as in the graph
above. The binomial expected column has the probabilities multiplied by
the total number of families, which is 1000.
The
Frequency column are the counts of numbers of families with each number
of boys - it is the observed data. The binomial probabilities are
calculated using the binomial formula, and are the same as in the graph
above. The binomial expected column has the probabilities multiplied by
the total number of families, which is 1000.
The Chi-square value is the (O-E)2/E calculated for each number of males, then summed.
Degrees of freedom are number of levels, which is 5, minus 1.
The p-value comes from comparing the calculated Chi-square value to a Chi-square distribution with 4 degrees of freedom. You can see the p-value is greater than 0.05, so we would conclude the observed frequencies match the binomial expected frequencies.
Conclusions to draw from a non-significant Chi-square GOF with binomial expected values
Remember, when we get a non-significant Chi-square test, we conclude that the data has the properties of the model that produced the expected frequencies. The important properties of the binomial distribution are:
- There is a single parameter, p, that applies to every trial - if the proportion of boys is p = 0.5, then every child has a probability of 0.5 of being a boy.
- The trials are independent - that is, if one child is a boy, it has no effect on whether any other child in the family is a boy, like coin tosses. If some fathers are more likely to produce male offspring and others are more likely to produce female offspring then the sexes of offspring wouldn't be independent, and the binomial wouldn't predict the distribution of numbers of boys well.
With a non-significant Chi-square test for these data, we would conclude that the probability of male children is 1/2, and that the sexes of children in families are independent of one another.
Lack of independence among trials
We can use a mismatch between our observed data and expected frequencies from the binomial to indicate that events were not independent, and lack of independence of events can be of interest to us scientifically. For an example of this approach, consider the apple.
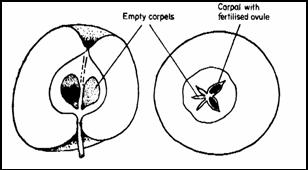 Apples
are the reproductive system of an apple tree, and apple seeds only
develop when they are fertilized by pollen.
Apples
are the reproductive system of an apple tree, and apple seeds only
develop when they are fertilized by pollen.
Apple pollen has to be carried from flower to flower by animals. For this example, we will stipulate that there are only two different types of potential pollinators for apples, bees and hummingbirds. Both animals pick up pollen while they feed on nectar from one flower and deliver it to the carpels of the next flower on which they feed. Bees are smaller than hummingbirds, and when bees visit an apple flower we might expect that it's possible for them to pollinate just a single carpel without pollinating any other. If this is true, the probability that any single carpel is pollinated should be unaffected by any other, each one like a flip of a coin.
The binomial distribution is based on the assumption that each event is independent, and thus bee pollination might be modeled well by the binomial. In contrast, because hummingbirds are much larger than bees, we would expect they will frequently touch all of the carpels at once when they visit a flower, or alternatively they may skip flowers entirely. Hummingbirds, then, may exhibit "all or nothing" patterns of pollination, in which pollination is not independent among the carpels (more like tossing five coins all taped together, with heads on the same side). This lack of independence would make hummingbird pollination a poor match to the binomial distribution. If this is true, then the distribution of apples with each possible number of pollinated seeds could look something like this:
| Apples with X seeds pollinated | ||
|---|---|---|
| Number of seeds pollinated | Bees | Hummingbirds |
| 0 | 0 | 15 |
| 1 | 1 | 6 |
| 2 | 7 | 4 |
| 3 | 15 | 3 |
| 4 | 27 | 11 |
| 5 | 25 | 36 |
| Totals | 75 | 75 |
To see how the binomial distribution compares to these numbers we need to know the probability that a single seed will be pollinated (p), and the total number of seeds in an apple (5). We can't assume that the probability of a seed being pollinated is 0.5, so we need to calculate it from our data.
To calculate p we just need to know the total number of seeds pollinated, and divide that by the total number of seeds possible across all the apples. The denominator is easy - there are 75 apples with 5 possible seeds each, which gives us 375 total seeds that could have been pollinated.
To calculate the total number of pollinated seeds from our table of frequencies, we need to: 1) multiply the number of seeds that were pollinated by the number apples with that number of seeds pollinated in the apples in that row of the table, then 2) sum the number of seeds pollinated across all the rows to get the total number of seeds pollinated across all the apples.
For the bee data, we get:
| Number of seeds pollinated | Apples with X seeds pollinated | Seeds pollinated |
|---|---|---|
| 0 | 0 | 0 x 0 = 0 |
| 1 | 1 | 1 x 1 = 1 |
| 2 | 7 | 2 x 7 = 14 |
| 3 | 15 | 3 x 15 = 45 |
| 4 | 27 | 4 x 27 = 108 |
| 5 | 25 | 5 x 25 = 125 |
| Total seeds pollinated | 293 |
So, the overall probability of a single seed being pollinated by a bee is 293/375 = 0.781.
Repeating this calculation with the hummingbird data gives us:
| Number of seeds pollinated | Apples with X seeds pollinated | Seeds pollinated |
|---|---|---|
| 0 | 15 | 0 |
| 1 | 6 | 6 |
| 2 | 4 | 8 |
| 3 | 3 | 9 |
| 4 | 11 | 44 |
| 5 | 36 | 180 |
| Total seeds pollinated | 247 |
The overall probability of a single seed being pollinated by hummingbirds 247/375 = 0.659.
Now that we have probabilities that a single seed will be pollinated, we can calculate the probabilities of each number of seeds pollinated out of the five found in an apple. For bees, the probability that an apple would have all five seeds pollinated would be:
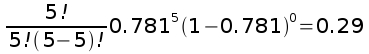
With this probability of 5 seeds pollinated the expected number of apples with 5 seeds pollinated is 0.29 x 75 = 21.79 apples - pretty close to the observed number of 25.
For hummingbirds, the probability of five seeds in an apple would be:
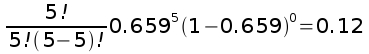
which, out of 75 apples, would be 0.12 x 75 = 9.32 apples - well below the observed number of 36.
|
|
|
|
Before we jump to conclusions, though, we should check what the Chi-square goodness of fit test says about how well the predicted numbers match the observed.
To do this, we just need to calculate a Chi-square value for the observed and expected numbers. First, for the bees:
| Number of seeds pollinated | Apples with X seeds pollinated (observed) | Binomial probability | Expected number of apples (prob x total apples) | (O-E)2/E |
|---|---|---|---|---|
| 0 | 0 | 0.0005 | 0.038 | 0.038 |
| 1 | 1 | 0.0090 | 0.675 | 0.156 |
| 2 | 7 | 0.0640 | 4.808 | 1.000 |
| 3 | 15 | 0.2285 |
17.138 | 0.267 |
| 4 | 27 | 0.4074 |
30.555 | 0.414 |
| 5 | 25 | 0.2906 | 21.795 | 0.471 |
| Totals | 75 | 1 | χ2 = 2.345 |
The Chi-square value is 2.345 for these data, which is the sum of the (O-E)2/E for each number of seeds pollinated. There are 6 different numbers of seeds, which gives us a degrees of freedom of 6-1 = 5. The probability of a Chi-square value of 2.345 if the null hypothesis is true is 0.7996 (which you can get from Excel or MINITAB). We would retain the null hypothesis that observed = expected, and find that the bee data fit the binomial distribution well.
Now the hummingbirds:
| Number of seeds pollinated | Apples with X seeds pollinated (observed) | Binomial probability | Expected number of apples (prob x total apples) | (O-E)2/E |
|---|---|---|---|---|
| 0 | 15 | 0.0046 | 0.345 | 622.519 |
| 1 | 6 | 0.0446 | 3.345 | 2.107 |
| 2 | 4 | 0.1722 | 12.915 | 6.154 |
| 3 | 3 | 0.3328 | 24.960 | 19.321 |
| 4 | 11 | 0.3216 | 24.120 | 7.137 |
| 5 | 36 | 0.1243 | 9.322 | 76.341 |
| Totals | 75 | 1 | χ2 = 733.578 |
The probability of a Chi-square value of 733.578 with 5 degrees of freedom is 2.69 x 10-156. We reject the null, and find that the hummingbird data do not fit the binomial distribution well.
What can we conclude from this exercise?
The bee data fits the binomial well, so we can conclude that bee pollination has the properties assumed by the binomial distribution. Specifically, the binomial distribution is based on the assumption that events are independent of one another, so our good fit to the binomial gives us support for the hypothesis that bees pollinate carpels independently of one another.
For the hummingbirds, the binomial is clearly a lousy model for the distribution of number of seeds pollinated in apples. The poor fit of the hummingbird data to the binomial distribution, along with the large number of 5 seeds and 0 seeds pollinated, supports our hypothesis that hummingbirds tend to either pollinate all of the carpels or none of them when they visit apple flowers.
So, the take-home points about the binomial are:
- Make sure you use expected values that accurately represent what your data would look like if they were randomly distributed among the categories - equal numbers or simple proportionality are not always to be expected.
- Fit or lack of fit to a model, like the binomial distribution, gives you some additional insight into the processes that generated the data. Good fit to a model is evidence that the data have the same properties as the model, and a poor fit to the model is evidence that the data do not share one or more of the model's properties.
Next activity
In the next activity we will practice using Chi-square goodness of fit testing using data on numbers of boys in families by birth order, and by doing the analysis of apple pollination using MINITAB.
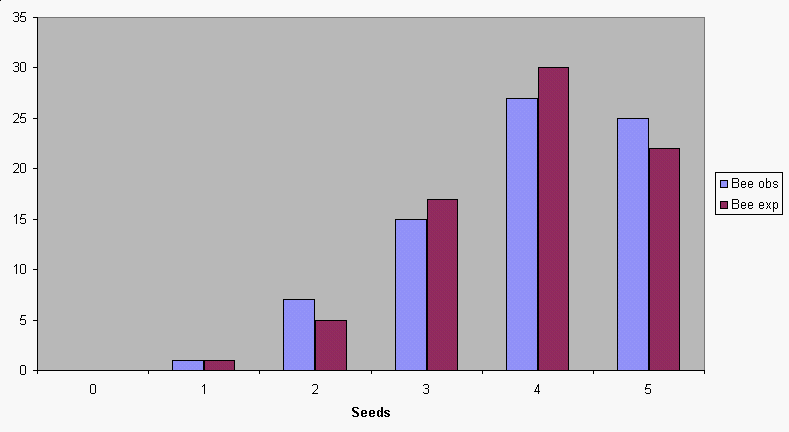 If
we do this calculation for all of the possible number of seeds
pollinated, from 0 to 5, we get this set of expected values. You
can see that the binomial distribution does a good job of
predicting the expected distribution of seeds for bees.
If
we do this calculation for all of the possible number of seeds
pollinated, from 0 to 5, we get this set of expected values. You
can see that the binomial distribution does a good job of
predicting the expected distribution of seeds for bees.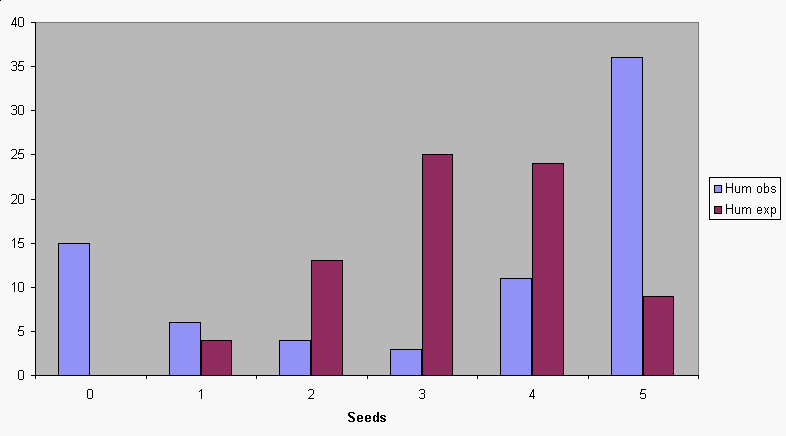 The
prediction is not very good for hummingbirds. Since we used the
probability that a seed was pollinated that we calculated from
the data, the mismatch can't be due to using the wrong
probability in our calculation. Instead, it is some other
characteristic of the binomial that doesn't represent
hummingbird pollination well.
The
prediction is not very good for hummingbirds. Since we used the
probability that a seed was pollinated that we calculated from
the data, the mismatch can't be due to using the wrong
probability in our calculation. Instead, it is some other
characteristic of the binomial that doesn't represent
hummingbird pollination well.