As you know, statistical tests only work when certain things are true about the data - the conditions that need to be met for the tests to work properly are called assumptions. General assumptions, like that data are randomly sampled and measured independently, are fundamental to drawing conclusions about populations from samples of data. When we use GLM, we base our interpretation on model coefficients, such as slopes and differences between group means. For our interpretation to be correct it's important that the GLM fits the data well - for example, predicted values should be in the middle of the data (at the group mean for grouped data, through the middle of the scatter of data for numeric predictors). We also rely on p-values to tell us which results to treat as real and which to treat as likely due to random chance, and for the p-values from a GLM to be accurate we need the data to be normally distributed and for the variances to be equal (HOV).

So far we have been treating assumption checking as a pre-flight check that we have to complete before we move on to fit a GLM. However, there's a big problem with this approach - whether the data meet assumptions of normality or HOV depends on the model.

Categorical predictor

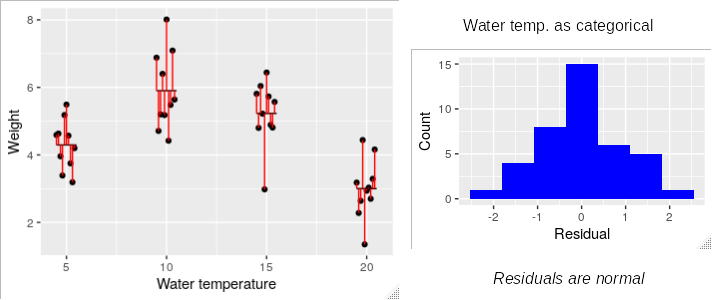
For example, if we have some data on the weight of some guppies grown at varying water temperatures we can treat temperature as a categorical variable with levels 5, 10, 15 and 20. Treating temperature as a grouping variable puts the mean for each group in the middle of the data, and the differences between data values and their group means (i.e. the residuals) have a nice bell-shaped distribution.

Click on the image, though, and you'll see what the model looks like if we treat water temperature as a numeric predictor instead. The line doesn't fit the data well, so there are many more residuals that are far from the line than when we treated water temperature as a categorical variable, and the histogram of residuals is skewed instead of bell-shaped.

If the model we use has an effect on whether we meet the assumptions or not we can't treat assumption tests as something we do first before analyzing the data.


What about homogeneity of variances? It isn't as obvious that the model we use would affect the HOV assumption, but it can.

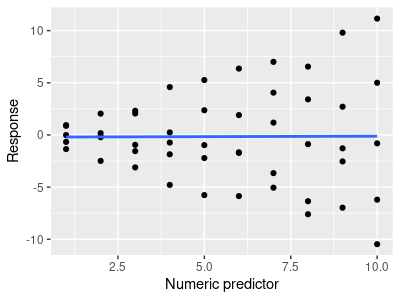
Non HOV

To see why this is the case, consider the simple example to the left of a simple linear regression of a response on a predictor variable. The HOV assumption for a regression is that the scatter around the line is equal from low to high predicted values. We can't even ask the question about whether a regression meets the HOV assumption until we have a line, which means we have to run the analysis to assess our compliance with the assumption.

But more than that, it's pretty clear from this illustration that variability increases from low to high values of the numeric predictor. However, if you click on the graph you'll see a different model that includes a categorical predictor (group) that has a strong interaction with the numeric predictor. If a model included both the numeric predictor and the groups, along with the interaction between them, the distribution of the data around the lines looks perfectly fine.


So, in both cases our conclusions about whether the data meet the assumptions of GLM depends on the linear model we are using - the same data may meet the assumptions of GLM with some models and not others. The implication of this is that we can't test our assumptions before fitting a model, we need to assess them by inspecting the residuals after the model is fitted.

For GLM to work well as a means of understanding our data, we need for the following to be true:

From now on, assumption checking will become part of the process of finding the correct model to use to interpret our data. This process is called model criticism.

Model criticism - finding the right model to interpret

There are a couple of common causes of violations of assumptions:

Incorrect model structure is illustrated above - leaving out predictors or interactions, or having a non-linear response can lead to violations of assumptions.

If we have responses that are multiplicative instead of additive we can still use GLM, but we need to apply a transformation first that changes the data to a log scale - multiplicative effects become additive on a log scale.

There are some additional sources of problems meeting assumptions, such as non-independence between measurements. We generally address this problem in our designs - we take pains to ensure that our measurements are independent of one another, and assume independence because we have left no opportunity for a lack of independence to affect our data. But, some common experimental designs produce data that lack independence, such as paired or repeated measures designs, and we can account for those issues in our analysis as well. Those complications are beyond the scope of this class, but I teach repeated measures analysis in my multivariate class.

Model criticism is the process by which we find the combination of model structure and data scale that allows us to meet GLM assumptions, and it goes as follows:

1. Fit a GLM model.

2. Examine the residuals for evidence of non-normality, heteroscedasticity (i.e. lack of homogeneity of variances), non-linearity, and lack of independence. We will see how each of the residual plots R provides lets you assess these assumptions when we first use them, below.

3. If any of these problems are detected, make a single change to the model (add a predictor variable, an interaction term, or apply a transformation).

4. Repeat steps 1-3 until the assumptions are met.

Bear in mind that it's okay to use an approach like this to find a model that meets GLM assumptions, but it would not be okay to use it to find a model that gives us the scientific results we want. Each time you fit a model you could in principle get an ANOVA table, coefficients, and/or Tukey tests, but you shouldn't - it isn't appropriate to interpret a model that doesn't fit your data, and the focus in model criticism should just be on whether you meet GLM assumptions.

Today's activity

We are going to analyze a data set presented in your book, which gives the results of a bacterial growth experiment. In this experiment, bacteria were grown in agar plates that contained all possible combinations of four levels of sucrose, and three levels of the amino acid leucine. Only one plate with each combination was used, so this is considered an unreplicated design, even though we get the "hidden replication" associated with our crossed design. Estimates of bacterial density (in cells per square centimeter) were made on four consecutive days, and bacterial density is the response variable. Bacteria reach staggeringly high densities, so the numbers range from the millions (e+06) to the tens of billions (e+10).

Start a new project, in a folder called "assumptions". Download this data file, and import it as the R dataset "bacteria". Download this Rmd file for your commands.

Convert the three predictors we will use (day, sucrose, and leucine) to factors. The data set from the book used numeric codes for days, leucine levels, and sucrose levels (as in 1,2,3,4 for the days), and it is particularly important to convert variables like this to factors so that R doesn't assume you want to use them as numeric predictors. I converted the levels in each of the variables to text labels, so this would not have been a problem for us, but it's a good habit to get into. I'll give you the first one - to convert day to a factor use (in the convert.factors chunk of your Rmd file):

bacteria$day <- factor(bacteria$day)

You'll see that the day variable now shows as a "Factor" instead of "chr" in your environment. Repeat this procedure with leucine and sucrose, just make sure you change the name of the variable on both sides of the assignment arrow.

Graphing the data:

It's a good idea to always start by looking at the distribution of the data, so let's make a histogram. You can do this with ggplot() using geom_hist() (in the plot.histogram chunk of your Rmd file):

ggplot(bacteria, aes(x = density)) + geom_histogram()

The data look very right-skewed. However, remember that the distribution of the data is not the important issue, it's the distribution of the residuals around the fitted model that determines whether we're meeting our normality and homogeneous variances assumptions. It's conceivable that once we have accounted for the effects of day, sucrose, and leucine that the residuals will meet our assumptions even if the raw data plot does not, so we need to fit a model before we can decide if we have a distribution problem. If the residuals are not okay, though, the right skew in the histogram here is a clue that we might want to consider a transformation.

First analysis:

Our first analysis will just reproduce the steps taken by the book.

1. Fit a linear model of density, with day, sucrose, and leucine included, but with no interactions, like so (in the fit.model.no.interactions.no.transformation chunk of your Rmd file):

dens.nointer.lm <- lm(density ~ day + sucrose + leucine, data = bacteria)

With no interactions in the model the predicted values will just be based on the main effects of day, sucrose, and leucine. You can see what the predicted values are with (chunk predicted.density of your Rmd file):

predict(dens.nointer.lm)

you will see:

          1           2           3           4           5           6
-2098253021 -1660590708  1817703042 -1469504938 -1031842625  2446451125
          7           8           9          10          11          12
  282183396   719845708  4198139458  1926983396  2364645708  5842939458
         13          14          15          16          17          18
-1368711354  -931049042  2547244708  -739963271  -302300958  3175992792
         19          20          21          22          23          24
 1011725062  1449387375  4927681125  2656525062  3094187375  6572481125
         25          26          27          28          29          30
 -722763021  -285100708  3193193042   -94014938   343647375  3821941125
         31          32          33          34          35          36
 1657673396  2095335708  5573629458  3302473396  3740135708  7218429458
         37          38          39          40          41          42
-1255042771  -817380458  2660913292  -626294688  -188632375  3289661375
         43          44          45          46          47          48
 1125393646  1563055958  5041349708  2770193646  3207855958  6686149708

These are the bacterial densities that the model predicts for each row in the bacteria data set - the numbers from 1 to 48 are the row numbers, and the large numbers below them are the mean densities expected for the combination of day, leucine, and sucrose found in each row. You'll notice there's already a problem - there are a lot of predicted means that are negative numbers, but density can't be negative. Since these predicted values are supposed to be group means they are clearly poor estimates, since they can't possibly be in the middle of data values that are all positive. Not a good sign, but we will withhold judgment until we see what the residuals look like.

We can calculate the residuals with (in chunk density.resids or your Rmd file):

residuals(dens.nointer.lm)

you will get the residuals:

          1           2           3           4           5           6
 2122953021  1698690708 -1512703042  1481704938  1121142625  -906451125
          7           8           9          10          11          12
 -258783396   238154292  2161860542 -1426983396 -1396645708 -3322939458
         13          14          15          16          17          18
 1460011354  1064049042 -2484344708   907963271   658300958  -325992792
         19          20          21          22          23          24
 -681725063  -512387375  1992318875 -2291525062 -1934187375  2147518875
         25          26          27          28          29          30
  725643021   301600708 -3042193042   126214938   -81647375 -3441941125
         31          32          33          34          35          36
-1357673396  4584664292 -1983629458 -2797473396 -2815135708  9781570542
         37          38          39          40          41          42
 1255825771   846380458 -2435913292   629434687   240932375  -409661375
         43          44          45          46          47          48
 -175393646 -1276055958 -2731349708   279806354 -2737855958  6513850292

These residuals are just the density data minus the predicted values from the model - you can confirm this by typing in the console:

bacteria$density - predict(dens.nointer.lm)

and you should get exactly the same values as you got with residuals(dens.nointer.lm).

Negative values are not a problem with residuals - a negative residual is just lower than its predicted value (in a model that fits perfectly about half of the data values will be less than their predicted values, because the predicted values are predicted means, and should be in the middle of the data).

We will use these residuals to assess normality and HOV, but there are some specialized residual plots that help us interpret them. We will get those plots next.

2. Residual plots for the fitted model are easy to get, but we will have to use base graphics to get them easily. We have been using the much prettier ggplot2 graphics throughout the semester, but it's a hassle to do these plots in ggplot(). This isn't really a problem, since plots of residuals are usually not presented in publications, and are mostly useful to you as the data analyst in assessing model fit. Even though they will be un-lovely, we will use R's base graphics to get our residual plots.

First, let's take a look at these graphs one at a time - in the console, enter:

plot(dens.nointer.lm)

You will see this residuals vs. fitted values plot:

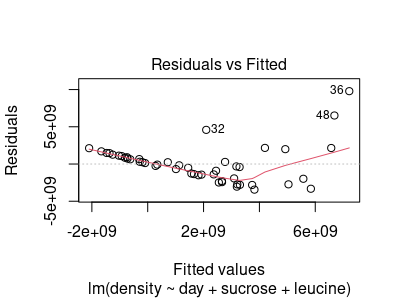
Resid vs fitted

Residuals are plotted against the y-axis, and the x-axis is the model predicted value (called a "fitted" value here). Points with numbers shown (like 36, 48, and 32) are unusual observations, that are more than 2 standard deviations from the predicted values (the numbers are row numbers, which help you identify which points have unusual values).

From this residual plot you can assess:

- Linearity = if the model fit the data well, the fitted values would be accurate estimates of the mean density at a given combination of day, sucrose, and leucine, and densities would vary normally around those means. Residuals would on average be 0 anywhere along the x-axis. The red line shows where the middle of the residuals is as you move from left to right, and the horizontal dotted line at 0 is the model predicted density - the red line is not flat at 0, so the model is not putting the predicted values in the middle of the data.

- Normality = the distribution of residuals around the line should be normal, so the data points should be symmetrical around the model predicted values, with points becoming less common as you move up or down away from the predicted values. The residuals are not symmetrical around 0, so we aren't meeting the normality assumption.

- Homogeneity of variances (HOV) = variability of the residuals around 0 should be equal as you move from left to right. If you divide the graph into four equal sections from left to right you would expect to see roughly the same amount of scatter within each section, but we're clearly getting much more variability at high predicted values compared to what we see at low predicted values. We do not meet the HOV assumption either.

If you hit Return you get the next graph, which is a normal probability plot (also called a quantile-quantile, or Q-Q plot):

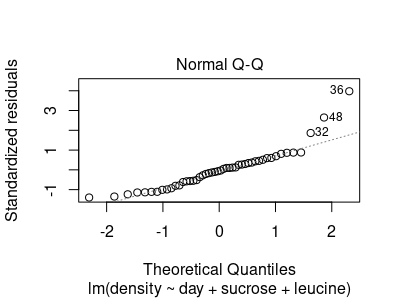
qq plot

This plot is exclusively used to determine if the data are normally distributed. The x-axis tells us how far from the mean we would expect the 1st data value to be (that is, the smallest), then the 2nd, 3rd, and so on, if our data were perfectly normally distributed. Then, we can use how many standard deviations each residual is from its predicted value (i.e. "standardized" residuals), and plot what we observe against what we expect. The diagonal dotted line is the line of perfect agreement between the observed standardized residuals (y) and the values we would expect from normally distributed data (x). The further the points are from the diagonal line the less reason we have to think the data are normally distributed. A random scatter around the dotted line is less problematic than deviations that form a pattern - there is an apparent curve to the residuals in this graph, which is strong evidence that the data are not normally distributed.

A Q-Q plot really doesn't tell us much about linearity or HOV. An concave upward curve like this is usually associated with positively skewed data, which suggests that a log transformation may be helpful, and log transformation affects both linearity and HOV as well as normality. But, the purpose of this graph is to assess normality.



If you hit Return again you will see a scale-location plot:

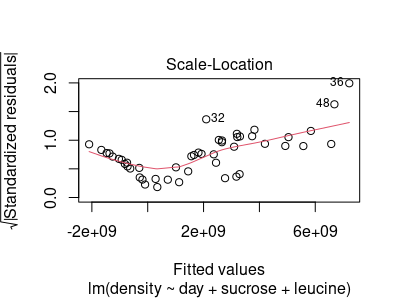
scale location

Like with the residual vs. fitted plot, the x-axis is the predicted value of cell density. The y-axis is the square root of the absolute value of the standardized residual. Using the absolute value of the residuals puts all of them above 0, and using the square root changes the scale in a way that makes spacing between small values easier to see. This plot is primarily useful for assessing HOV - you would expect an even amount of variation around the middle of the points (indicated by the red line) as you go from left to right. What we see here is almost no variability at low fitted values, and more variability as you move to big fitted values - not an equal amount of variation, so we do not have HOV.



Hitting Return one more time gives us a leverage plot:

leverage

Leverage refers to how influential a data value is on the estimate of a slope in a regression. We don't have much use for it here, but R includes it by default for all GLMs.



Now that you know what these are and how to interpret them, it's convenient to get all four of them reported at once in our knitted output. To get this, we need to tell R that we want two rows and two columns of graphs as output so that all four graphs will be plotted together.

We set graphical parameters in R base graphics with the par() command. If you type par() in the console you'll see a long list of cryptic codes and numbers that set various default properties of R's graphs. We want to be able to restore these default settings when we're done, so use the command (in the plot.residuals.from.first.model chunk of your Rmd file):

oldpar <- par()

This puts a copy of all the default settings into the object oldpar - to restore these default settings we will just use the command par(oldpar), and everything will be back to normal.

To tell R that we want to a) plot all four graphs as panels in a single graph, and b) make room for a label for the model that's being plotted, we need to set the numbers of rows and columns of plots to create (for a), and to set the margins (for b). The command is (in the same chunk):

par(oma = c(0,0,3,0), mfrow=c(2,2))

The oma parameter is the outer margin in order bottom, left, top, right - we're adding some space to the top for the model statement to be printed. The mfrow parameter gives the number of rows and columns of panels to be used in the plot - we'll have 2 rows and 2 columns, so all four of the plots will be presented at once. The par() command sets these parameters internally, so we don't need to assign the output to anything for them to take effect.

Now, to get the plots, use the command (in the same chunk):

plot(dens.nointer.lm)

and you'll see all four of the residual plots grouped together below the code chunk.

You are encouraged to learn to rely on these plots to decide whether you meet GLM assumptions eventually, but the decisions about whether assumptions are being met may seem uncomfortably subjective to you at this point. The book's advice is to not be too picky, but as you are learning what constitutes acceptable levels of deviation from assumptions you can use some familiar assumption tests to double-check your impressions of the graphical diagnostics.

Potential violation of assumptions

Quantitative test

Lack of normality

Shapiro test of normality. The Shapiro test can be run through the Script Window with the command (in the shapiro.bp.test.first.model chunk of your Rmd file):

shapiro.test(residuals(dens.nointer.lm))

This command first extracts the residuals from dens.nointer.lm using the residuals() command, then feeds the residuals into the shapiro.test() command to test for normality. This is a hypothesis test, with the null hypothesis being that your data are normally distributed. Consequently, a p greater than 0.05 indicates normality, because retaining the null hypothesis means concluding your data are normal.

Lack of homogeneous variances

The Breusch-Pagan (BP) test of homogeneity of variances is also available.

This test is found in the lmtest library - you will need to install it the first time you use it. Once lmtest is installed, load it with library(lmtest) and use the command (in the same chunk):

bptest(dens.nointer.lm)

The null hypothesis for this test is that your data has equal variances, so a p greater than 0.05 indicates that you've met the assumption.

3. At this point you should see that the model assumptions are not met, and we need to do something differently.

The first attempt to fix our distributional problem will be to add an interaction between sucrose and leucine. Interactions allow the predicted values to get closer to the observed data, which can help with linearity, and when the model predicts the means well you will sometimes fix apparent non-normality and lack of HOV problems too.

Fit a model that still uses day as a block (that is, with no interaction), but has a sucrose*leucine interaction. Call the model dens.inter.lm (put this command in the interaction.sucrose.leucine of your Rmd file).

4. Produce your diagnostic plots for this model (in chunk plot.residuals.from.second.model of your Rmd file), and run the quantitative tests to confirm your impression (in chunk shapiro.bptest.second.model of your Rmd file). You'll see that we're not out of the woods yet, we need to try another fix.

5. Next we will try log-transforming the densities. We might expect that log transformation will help because the densities were right-skewed in our histograms - we have two choices for making R use a log-scale response:

The second approach is the simplest, in that it only requires us to make a simple change to the lm() statement - we can use the command (in chunk log.density of the Rmd file):

dens.inter.log.lm <- lm(log(density) ~ day + sucrose * leucine, data = bacteria)

This will cause R to log-transform the densities for analysis without changing the data in the bacteria data set. In R, log() is the natural log, whereas log10() is the log base 10. The base you use won't affect the result, so we will use the natural log - it's important to know which base you used so that you can back-transform your results correctly.

6. Produce your diagnostic plots for this model (in the plot.residuals.from.third.model chunk of your Rmd file). As your book points out, after transforming the data and including an interaction, you have produced a good looking set of diagnostic plots, with only minor deviations from model assumptions. Confirm this impression with a Shapiro test for normality of the residuals, and a BP test for homogeneous variance (shapiro.bptest.third.model chunk) - we pass both of them.

Second analysis:

The first analysis just repeats the example used in your book, and for the most part the book does a good job of explaining the steps and illustrating the process. However, they do leave out one interesting issue, so we will address it now: which treatment for violations of assumptions should we try first? And, when the first treatment doesn't fix our problems, why should we apply the second treatment on top of the first, rather than applying the second treatment instead of the first?

Given the highly skewed distribution of the data, it's not surprising that log transformation was effective in helping us meet GLM assumptions, and it's entirely possible that a log transformation is all we need to do - the interaction between sucrose and leucine may be an unnecessary step (note that the interaction becomes non-significant after the data are log-transformed).

To address this question, fit one more model using the log of density, but with only main effects of day, sucrose, and leucine (call it logdens.nointer.lm, in log.but.no.interaction chunk of your Rmd file). Produce the diagnostic plots for this model (plot.residuals.from.fourth.model chunk of the Rmd file), and see whether there are distributional problems still evident. Run the BP and Shapiro tests to confirm your impressions of the graphical diagnostic plots (shapiro.bp.fourth.model chunk of the Rmd file).

Based on your graphs and assumption tests you should find that log transformation is all that is needed to meet GLM assumptions - the interaction was not necessary. The book tried an interaction, found it didn't fix the distribution problems, and then log-transformed density and fit a model that included the interaction between sucrose and leucine. They didn't have to keep the interaction in, so why did they?

What the first and second analysis show us is that there are two different models of log-transformed densities that meet GLM assumptions, one with an interaction between sucrose and leucine and one without. The reason we would want to try the leucine x sucrose interaction first, and keep it in even after it didn't solve the distributional issues, is that we are interested in the interaction scientifically. Trying it first makes sense in that it was possible that all we needed to do to fix the residuals was to add an interaction, without log transformation. If that had been the case, we would have had our test of the interaction included, and wouldn't have had to deal with the complication of having to interpret log densities. Even when it became clear that log transformation was necessary, we still wanted to know if the interaction was significant, so it made sense to keep it in the model. If instead we had fit this logdens.nointer.lm model we would have found that the residuals were fine, but we still wouldn't know if the interaction was significant, and we would have had to fit a model with that interaction included anyway.

So, even though they didn't explain their reasoning completely, the way the book approached their model criticism of the bacteria data made good sense.

What does it all mean? Interpreting analysis of log-transformed data.

Sometimes researchers use log-transformed data for their statistical testing, and then present their results using arithmetic means. This is the simplest choice for the researcher, but it obscures the relationship between the data analysis and the data that's presented for interpretation. Sometimes this can even lead to the appearance that you've done something wrong.

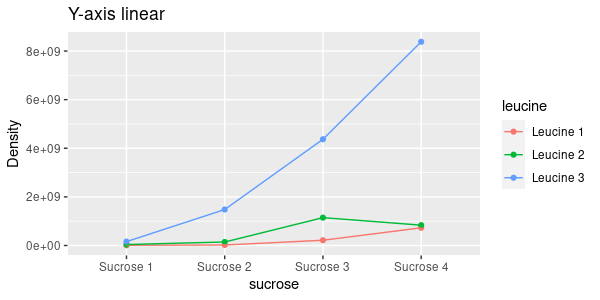
Predicted values

For example, the interaction plot to the left shows the densities for the combinations of leucine and sucrose. As you now know, when you see lines on an interaction plot that are not parallel you should expect a statistically significant interaction between the predictors. You weren't supposed to get an ANOVA table for your models until you passed assumptions, but if you had (by typing anova(dens.inter.lm) in the console) you would have gotten:

Response: density
                Df     Sum Sq    Mean Sq F value    Pr(>F)   
day              3 1.1546e+19 3.8487e+18  0.8119 0.4964173   
sucrose          3 1.1872e+20 3.9574e+19  8.3488 0.0002865 ***
leucine          2 1.4733e+20 7.3666e+19 15.5411 1.755e-05 ***
sucrose:leucine  6 1.3440e+20 2.2400e+19  4.7257 0.0014198 **
Residuals       33 1.5642e+20 4.7401e+18 

The sucrose:leucine interaction is significant before we transform the data.

If you click on the graph you will see the y-axis changes to the log of density. This is what we use for analysis, and the lines are now more or less parallel. Because of this if we get the ANOVA table for the model that used log density, (anova(logdens.inter.lm) in the console):

Response: log(density)
                Df  Sum Sq Mean Sq F value    Pr(>F)   
day              3   5.547   1.849  1.3826    0.2653   
sucrose          3 110.466  36.822 27.5330 4.164e-09 ***
leucine          2  80.473  40.237 30.0863 3.649e-08 ***
sucrose:leucine  6   6.091   1.015  0.7590    0.6071   
Residuals       33  44.134   1.337

The sucrose:leucine interaction isn't significant on a log scale because the lines are nearly parallel on a log scale. If you did the analysis on a log scale, but presented graphs with the data on the original, linear density scale you would present a graph with what looks like a pretty obvious interaction along with an ANOVA table that shows it to be not statistically significant. If instead you present the graph of log-density your statistical results will match your graph, which is much more clear and less confusing.

The only issue with using the log of density on the y-axis is that it's hard to relate the results back to the real world - we can see from the graph that the combination of Sucrose 3 and Leucine 3 gives a mean log density of a little more than 22, but it isn't so clear what a log density of 22 actually means - we would have to do the math to back-transform this number into units of cell density to understand it properly. A good alternative is to use a log-scaled y-axis - click once more and you'll see the same graph with a log-scaled y-axis. The ticks along the y-axis are evenly spaced, and are all an order of magnitude apart - the lowest tick is 1e+07, the next is ten times as big at 1e+08, the next is another ten times as big at 1e+09, and so on. This axis scaling shows what the pattern is on the scale that we did the analysis (i.e. relatively parallel lines, without an interaction between sucrose and leucine), but the axis labels are in the same units as the data (density, instead of log of density). This version of the graph is a good way to display what your model tested for, in a way that is easily interpreted.

Let's see how we get what we need to properly interpret our results.

Getting the statistics you need to interpret model results

Getting the means, error bars, and graphs we need to interpret analysis of log-transformed data involves back-transforming from a log scale back to the original data scale. A little review of transformations and back-transformations, and what they do to our analysis:

Transformation changes what type of mean the model is predicting

Linear models predict the arithmetic mean of y based on the values of the predictors. If we are using log-transformed responses, then the linear model predicts the arithmetic mean of the log of the responses. However, the arithmetic mean of log-transformed data is actually a geometric mean in the original data units. Geometric means are the nth root of product of n data values. Using arithmetic means of log-transformed data is equivalent to using geometric means in the original scale of the data.

The function that reverses natural log-transformation is the exp() function, which is the base e raised to the power of the value entered into the parentheses. We can calculate our group means of log-densities, and then back-transform them using exp() to get geometric means in the original data units of density.

Let's look at a simple example of a model that only includes sucrose, with log-transformed densities. The coefficients for this (significant) model are:

Coefficients:
(Intercept)     sucrose2     sucrose3     sucrose4 
     17.443        1.484        3.307        3.823 

As always, the intercept is the mean of the baseline group, which in this case is sucrose1. If we wanted to know what density this value of 17.443 was equivalent to, we just need to use exp(17.443), which is equal to a geometric mean density of 37,618,255 cells per ml.

That's simple enough, but we have sucrose2, sucrose3, and sucrose4 as well. We can get the predicted means on a log scale for these groups like so:

sucrose2 = 17.443 + 1.484 = 18.927

sucrose3 = 17.443 + 3.307 = 20.750

sucrose4 = 17.443 + 3.823 = 21.266

When we use log-transformed data, adding these coefficients on a log scale is equivalent to multiplying them in the original data scale.

For example, to calculate the predicted bacteria density in sucrose level 2, we could calculate the predicted value on the log scale and back-transform, like so:

GMsucrose2 = exp(17.443 + 1.484) = e17.443e1.484 = 37618255 x 4.41 = 165,917,295 cells per ml

Main effects of sucrose and leucine

If we fit a model of main effects of sucrose and leucine with log-transformed densities, we get the coefficients:

Coefficients:
(Intercept)     sucrose2     sucrose3     sucrose4     leucine2     leucine3 
     15.953        1.484        3.307        3.823        1.314        3.157  

Now, if we want to know the geometric mean predicted for sucrose 2 and leucine 2, we would either calculate:

GMsucrose2, leucine2 = exp(15.953 + 1.484 + 1.314) = 139,141,227

Now that you see how the back-transformed geometric means are calculated, we can use the emmeans library to do much of the work for us. All of these calculations can be done with R functions, but the emmeans library makes them much more convenient.

1. Load the emmeans library (load.emmeans chunk of your Rmd file):

library(emmeans)

2. The emmeans() command will do all the work for us - using it without specifying a "type" will give us the means for each leucine level on the scale used by the model, which is the log of density (log.scale.leucine chunk of your Rmd file):

emmeans(logdens.nointer.lm, specs = "leucine")

This will give you the output table:

 leucine   emmean    SE df lower.CL upper.CL
 Leucine 1   18.1 0.284 39     17.5     18.7
 Leucine 2   19.4 0.284 39     18.8     20.0
 Leucine 3   21.3 0.284 39     20.7     21.8

Results are averaged over the levels of: day, sucrose
Results are given on the log (not the response) scale.
Confidence level used: 0.95

The specs = "leucine" argument tells emmeans() that we want the marginal means for leucine. Since we used log(conc) as our response variable, emmeans() was able to infer that the data were on a log scale without our telling it explicitly - you'll see that the output reports that these means are on a log scale.

We can get this output for more than one of the predictors at a time - in the console enter the command:

emmeans(logdens.nointer.lm, specs = list("leucine","day"))

This will give you a table of least squares means for both leucine and day.

3. To get plots of the log-transformed means, with 95% confidence intervals, use the command (in chunk plot.log.leucine.linear.y of your Rmd file):

emmip(logdens.nointer.lm, formula = ~ leucine, CIs = T) + labs(y = "Log of Density")

This first plot command plots the log of bacterial density on the y-axis, and the three levels of leucine on the x-axis, with plot symbols for the (geometric) means, and 95% confidence intervals as error bars. Using the labs() command is used to change axis and title labeling, and we are setting the y-axis label to "Log of Density" to reflect that these numbers are the log of the density values.

4. To get the table of means back-transformed to density, we just need to change the emmeans() command to add type = "response" (in the linear.scale.leucine chunk of your Rmd file):

emmeans(logdens.nointer.lm, specs = "leucine", type = "response")

The table is laid out the same way, but now the means (in the "response" column) are back-transformed values, and are thus the geometric mean density for each leucine level.

 leucine   response       SE df lower.CL upper.CL
 Leucine 1 7.30e+07 2.07e+07 39 4.11e+07 1.30e+08
 Leucine 2 2.72e+08 7.71e+07 39 1.53e+08 4.82e+08
 Leucine 3 1.72e+09 4.87e+08 39 9.67e+08 3.05e+09

Results are averaged over the levels of: day, sucrose
Confidence level used: 0.95
Intervals are back-transformed from the log scale

It's hard to see that the confidence intervals are asymmetrical, but the graph will make this clear - the confidence interval is calculated from the log of density and then back-transformed, which results in lower limits that are closer to the geometric mean than the upper limits are.

5. Plotting the results on the response scale is done with (in the plot.leucine.linear.y chunk of your Rmd file):

emmip(logdens.nointer.lm, formula = ~ leucine, CIs = T, type = "response") + labs(y = "Density")

Using type = "response" sets the y-axis to a be a linear, un-transformed scale, and uses the back-transformed means and confidence intervals.

Now you can see clearly that the confidence intervals are asymmetrical in this plot. Asymmetrical confidence intervals should make sense to you - the densities have a basement at 0, but can extend to huge numbers. Because of this, our estimates of geometric means shouldn't be allowed to be negative numbers, which means that we can't be off by as much in the negative direction as we can be in the positive direction. The longer interval in the positive direction reflects this asymmetry in our uncertainty.

None of these graphs is a bad choice - all of them at least plot the geometric means instead of the arithmetic means, such that the means plotted match the means compared by the model. If you use the type = response graph you emphasize the real-world interpretation of the results, including the asymmetry in uncertainty of the estimated means, but you give the impression that there is an interaction between leucine and sucrose that you would report to be non-significant. If you use the type = link version you show exactly what was analyzed, including the log-density means, but at the cost of having less easily interpreted summary statistics. The default graph, with a log-scaled y-axis is a nice compromise between presenting the patterns that were actually analyzed, but using axis labeling that is easy to interpret. But, as long as you understand and explain what the graph is showing, any of the graphs could be used to illustrate the model.

Alternatively, you may want to plot back-transformed densities, but use a log-scaled y-axis. The information in the graph will be the same as in the linear scaled graph you just made, but the spacing between the ticks on the y-axis will be based on their log-transformed values - the numbers will reflect the densities, the points on the graph will be geometric means, but the confidence intervals will be symmetrical. In the console enter:

emmip(logdens.nointer.lm, formula = ~leucine, CIs = T, type = "response") + labs(y = "Density") + scale_y_log10(breaks = seq(1e+08, 3e+09, by = 1e+08))

This version of the graph has y-axis units of density, but the y-axis is log scaled. We're setting the ticks manually withe the breaks = seq(1e+08, 3e+09, by = 1e+08) argument - this makes a sequence of numbers starting with 100,000,000 and ending with 3,000,000,000, and adding 100,000,000 each time - if we just used the seq() command at the console you would get the sequence:

 [1] 1.0e+08 2.0e+08 3.0e+08 4.0e+08 5.0e+08 6.0e+08 7.0e+08 8.0e+08 9.0e+08 1.0e+09 1.1e+09
[12] 1.2e+09 1.3e+09 1.4e+09 1.5e+09 1.6e+09 1.7e+09 1.8e+09 1.9e+09 2.0e+09 2.1e+09 2.2e+09
[23] 2.3e+09 2.4e+09 2.5e+09 2.6e+09 2.7e+09 2.8e+09 2.9e+09 3.0e+09

The values are all evenly spaced, but on the graph the spacing between them gets increasingly small as you increase on the y-axis - this is because log axes are scaled so that the distances between multiples of 10 are the same. So, for example, the spacing between 1.0e+08 and 1.0e+09 would be the same on the graph as the spacing between 1.0e+09 and 1.0e+10. Using a log-scaled y-axis is a compromise between displaying the scale on which the analysis was done, and the scale of the data - the pattern of change between the means, and the confidence interval widths, are all the same as in our first graph of the log-transformed data, but you can read the actual densities from the y-axis labels.

The y-axis labeling makes the point about what the values represent, but there are way to many to actually read - so, as your final command in the plot.leucine.log.y chunk of your Rmd file enter:

emmip(logdens.nointer.lm, formula = ~leucine, CIs = T, type = "response") + labs(y = "Density") + scale_y_log10()

This final version of the graph uses ticks that are all 3x each other (that is 3e+08 is three times as big as 1e+08, and 1e+09 is three times as big as 3e+08) - not quite orders of magnitude, but since the data cover less than two orders of magnitude there wouldn't be enough ticks if we used factors of 10.

Wrapping up with some advice

You used model criticism to produce two different models that satisfied the assumptions of GLM. So, which is the better way to proceed? It depends on the goals of your analysis, but a few things to consider:

That's it! Knit and upload your Word document.