Next week we will learn to use likelihoods of models as the basis for drawing scientific conclusions, using the method of support. To prepare you to use this new approach we will spend this week working with likelihoods to better understand how they are calculated, and what they tell us about our models. The examples we use today make use of things you already know how to do in R, like calculating a mean and fitting a regression line to some data, but we will use these familiar methods this week to learn about likelihood.
We will start by using the same example as we used in lecture of estimating the mean from a set of data. We will start with several web-based apps, below, to learn what you need to know about how likelihood works, and then we will implement the same procedures in R Studio. We won't need it right away, but go ahead and start a new project (called "likelihood"), and download this Rmd file and this Excel spreadsheet file into it. We won't need to import anything quite yet, the instructions will let you know when it's time to do so.
Numerical maximum likelihood estimate of the mean
The methods we use today are examples of numerical methods, in the sense that we will try out different possible values for unknown parameters and see which ones maximize the likelihood function. Numerical methods are a real technique for finding solutions, but the actual numerical methods used in real data analysis are more sophisticated than we will use here. Using graphs is a good way to understand the concepts, though, so that's what we will do.
This first app allows you to try out different possible estimates for the mean by sliding the slider button right and left - the current estimate is listed above the slider. The likelihood of the estimate of the mean given each individual data value is illustrated in the graph to the left - the normal curve over each data value is its likelihood function, and drawing a line vertically from the value of the estimate to the curve shows the likelihood of that estimate given each individual data point. Multiplying these all together gives you the value on the likelihood function to the right - the dot on the curve is the likelihood given all the data for the current estimate. Changing the estimate by moving the slider gives you different heights on the individual likelihoods - they all peak at the data value, so the maximum likelihood estimate given any single data value is equal to the data value itself. However, maximizing the likelihood for one point will lead to lower likelihoods on others, and across all the data the value that maximizes the products of all the individual likelihoods may not be equal to any single data value. The goal is to find the value of the mean that maximizes the likelihood of the entire data set, so you will want to move the slider until the dot on the right graph is at the top of the curve.
1. To get a feeling for how this works, slide the slider to 119.4 - this is the value of the smallest data point. You will see that the likelihood for the data point at 119.42 maximizes, but since 119.4 isn't close to any of the other data values they all decline substantially.
Click on the camera icon at the top of the Likelihood functions for
each point graph (which appears when you hover over the graph,  , and download a picture of your graph to the
project folder. It is VERY IMPORTANT to use the right file name so that
it will show up in your Rmd file properly - this file should be called
mean_119_individual.png.
, and download a picture of your graph to the
project folder. It is VERY IMPORTANT to use the right file name so that
it will show up in your Rmd file properly - this file should be called
mean_119_individual.png.
If you look at the dataset likelihood function you'll see that 119.4 has a very low likelihood given all the data. Maximizing the likelihood with respect to a single data value is resulting in a low likelihood with respect to the entire data set, because the likelihood is low for many of the indiviudal points.
Click on the camera icon at the top of the top of the Likelihood function of dataset, and download the file with the name mean_119_dataset.png.
2. Now use the slider to find the value for the mean that maximizes the likelihood given the dataset - the red dot will be at the peak of the dataset curve.
Click the camera icon for each graph - call the individual one mean_ml_individual.png, and the dataset one mean_ml_dataset.png.
Note that if you hover over the red dot sitting at the peak of the dataset likelihood function it has a likelihood of 1.068 x 10-18. This is obtained by multiplying each of the individual likelihoods together, and since the individual likelihoods are obtained from normal curves it seems like the likelihood might indicate some sort of probability of the data set, but that's not the case. There are a couple of reason we don't interpret likelihoods as probabilities:
- First, the normal curve is a probability distribution for a continuous variable. The height of the curve at a point for a continuous probability distribution is not a probability - it is a probability density. Probability distributions have an area beneath them equal to 1, such that the area beneath the curve between any two values along the x-axis will be between 0 and 1, and can be interpreted as a probability of an outcome falling between the two x-values. To calculate an area we need both a width and a height - we have a height (the vertical distance from 0 to the curve), but a single data value is a point along the x-axis does not have a width, so we cannot calculate the area under the curve for a single data value. Probabilities of single values are undefined for continuous variables, we can only calculate probabilities for ranges of values. So, when we use the normal curve as a likelihood function we are using the probability density of each point as its likelihood, and we can't interpret that as a probability of that data value.
- Even if we got around this problem somehow, it is possible to use a
version of the normal likelihood function that doesn't even give
probability density. For example, the normal log-likelihood is
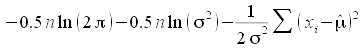 , and if we treat the standard
deviation as a known quantity we can drop the first two terms, and
just use
, and if we treat the standard
deviation as a known quantity we can drop the first two terms, and
just use 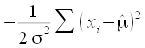 - this is still a likelihood function, and it still peaks at the same
place, but without the other terms the area under the curve is no
longer 1. Since the area beneath the curve isn't 1, this likelihood
function is no longer a probability distribution.
- this is still a likelihood function, and it still peaks at the same
place, but without the other terms the area under the curve is no
longer 1. Since the area beneath the curve isn't 1, this likelihood
function is no longer a probability distribution. - It is important to keep in mind that probabilities take the parameters (mean and standard deviation) as givens, and calculate the probability density of the data, whereas likelihood takes the data as givens, and calculate the likelihood of the parameter values. What we consider to be known vs. unknown is different for these two different uses of the normal distribution, and it's best not to confuse them by treating the likelihood as though it indicates probability.
So even though we use a probability distribution as our likelihood function, we can't interpret the likelihood as a probability.
This is important, because probabilities have meaning as single values. Knowing the probability of getting a heads from a single coin toss is 1/2 tells us something about what to expect when we toss a coin - the number is meaningful by itself. However, likelihoods are not meant to be interpreted as single values, they are only meaningful in comparison with other likelihoods. Thus, the fact that 1.068 x 10-18 is the biggest likelihood possible for any value of the mean given the data set is meaningful, but the actual numeric value of the likelihood doesn't tell us anything in particular.
3. Now to see how the likelihood function looks on a log scale, select "Log likelihood" from the drop-down menu below the slider (keep the mean at its maximum likelihood value). You will see that the location of the maximum didn't change, and there is still just one maximum value, but the y-axis now shows the natural log of the likelihood. Since natural logs are exponents needed to raise the base, e, to equal the data value they are all negative - all the likelihoods are small decimal numbers, so it requires negative exponents to represent them.
Click the camera icon just for the dataset graph (since nothing changed for the individual likelihoods) and save the file as mean_loglike_dataset.png.
4. Interpreting negative values can be inconvenient, so we often express log likelihoods by multiplying them by -1. This flips the curve so that it points upward, such that the maximum likelihood estimate is at the minimum of the negative log likelihood. To see this, select "Negative log likelihood" from the menu, and you'll see that the log likelihood graph for the dataset flips around the x-axis, and points upward. The y-axis scale has the same numbers, but are all positive, and the x-axis value at the minimum is the same as the x-axis value at the maximum of the likelihood or log likelihood graphs.
Okay, now that you know that this "numerical" approach that you used to find the top of the likelihood function by trial and error produces a maximum likelihood estimate for the mean of 127.8, what does is the mean of the data using the analytical formula? Import the worksheet "EstimateMean" from the "likelihood_data.xlsx" Excel spreadsheet, and calculate the mean of the Data column - R's mean() function uses the usual analytical formula for the mean. You should see that it's equal to the maximum likelihood estimate you obtained (to the one decimal place we were able to estimate with the web app, at least).
Maximum likelihood estimation of the slope and intercept of a regression line
The first example of estimating the mean of a sample of data was (relatively) easy to understand, but doesn't really do much useful work for us. We are working in the direction of using likelihood as the basis for making comparisons between models that represent different hypotheses about our data, and the next step is to use likelihood to estimate the slope (β) and intercept (α) of a linear regression model.
Using a straight line, with a slope and an intercept to estimate, seems like it would complicate the likelihood function, but it doesn't - the only thing we need to do differently is to use the predicted value of the regression model instead of the estimate of the mean in the likelihood function. The log likelihood function looks like this:
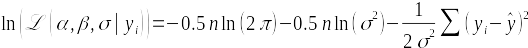
The cursive L is the symbol for likelihood. The parameters we are estimating are on the left side of the vertical line in (α,β,σ), meaning they are unknowns, and the data value (yi) on the right side of the vertical line are treated as known. The log-likelihood function has terms for the sample size (n), the variance (σ2), the predicted value of y (ŷ), and the data values (yi). Since yi - ŷ are the residuals for the regression line, we will maximize the likelihood by making the residuals as small as possible across the entire data set.
Notice that the two parameters we want to estimate, β and α, aren't in the likelihood function. This is because we won't be maximizing the likelihood of β or α individually - instead, we will be maximizing the likelihood of the linear regression model as a whole. The parameters are used to calculate the predicted values, ŷ, and thus we can change the estimates of the slope and intercept and see how this changes the likelihood of the model.
The other parameter in the log likelihood that we need to be concerned with is σ, the standard deviation of the residuals - to simplify this example we'll treat it as a known value, which I estimated in R based on the residual sums of squares for the model.
Although the likelihood function is nearly the same as the one we used
to estimate the mean of a data set, the app below looks a little
different. The graph on the left shows the data points as a scatterplot
of y and x values (a response and a predictor variable of some kind),
but the likelihood functions for each individual data value are plotted
as a third dimension, along the z-axis. The graph on the right is the
likelihood function (z axis) for ranges of possible values for the slope
(x axis) and intercept (y axis). As you pick better values for the slope
and intercept the red dot showing the likelihood of the currently
selected slope and intercept will climb up the likelihood surface - if
you over over the top of the surface you can get an idea of what the
best slope and intercept estimates are and enter those.
|
Slope: Intercept: |
1. To get started, let's make sure you're clear about what the graph on the left shows. Rotate the graph so that the predictor is horizontal, and the response is vertical, with the likelihood pointing out of the page - it should look more or less like the typical 2-dimensional scatterplot, but with colored points. Initially the slope is set to 0 and the intercept is set to the mean of the response data (8.82), so it is a not very well-fitting horizontal line through the data. Just like with any other regression, we are interested in finding the line that fits the data best.
You may notice in this orientation that there seems to be a bit of a non-linear pattern in the data - possibly an upward curve would fit better than a straight line. We will deal with that complication in the next version of the app.
If you start increasing the slope (by clicking the up-arrow in the box next to the Slope box) you'll see the line starts to tilt upward. The intercept is still at the mean for the data, so as you tilt the slope upward it pivots at the y-axis value of 8.82, and quickly starts to leave the data. As you do that the likelihood gets smaller, because the line passes under the low parts of the individual point likelihoods.
Once the line is above all the data you can bring it down into the data again by reducing the intercept - this will cause the line to move down without changing the tilt. As you move it into the data again you'll see the likelihood increases again because the line is passing under the taller parts of the likelihoods.
Rotate the graph so you can see the normal likelihood curves, and you'll see the vertical lines connecting the regression line to the curves - these are the individual likelihoods. Just like with the estimation of the mean, above, each of these individual likelihoods is multiplied together to give you the dataset's likelihood. The likelihood for the whole dataset is reported in just below the title for the graph. As you change the slope or intercept you'll see that as the line moves under the curves the lines change height - the goal is to get them as high as possible collectively across all the points.
2. Turn your attention to the "Likelihood function" graph to the right. This graph gives the likelihood of combinations of slope and aspect that you could select. If you move your mouse over the surface you'll see a popup that gives the slope, intercept, and likelihood for the model that uses that slope and intercept.
If you run your pointer over the top of the curve you'll see that the likelihoods peak at a slope of about 0.27 and an intercept of about 5.3. If you rotate the graph you'll see that the likelihood function is very narrow - this is because the slope and intercept work together to get the line into the data, and if you set the slope to 0.27 while the intercept is different from 5.3 you won't get a high likelihood for the model (or, if you use an intercept of 5.3 with a slope that's different from 0.27 you get the same problem).
You can switch to a log likelihood surface by selecting that option from the drop-down menu above the likelihood function graph. You'll see that it's shaped differently, but the maximum is in the same location (it's harder to find because it's pretty flat along the top of the surface the way I plotted it). Just like before, though, there is just one highest point, so there is a single best slope and aspect combination for this model.
Switching to a negative log likelihood flips the log likelihood over, and the minimum of the negative log likelihood is the maximum likelihood for the model.
3. Now that you know roughly what the maximum likelihood estimates will be for the slope and intercept, enter them into the boxes (0.27 for the slope, 5.3 for the intercept). When you do this you'll see that the regression line gets much thicker and turns bright red to indicate that you're close to the best value. The actual maximum likelihood possible for this straight line is 1.29 x 10-5, so fiddle with the slope and intercept to get as close to this model likelihood as you can.
When you have the best slope and intercept you can get click on the camera icon and download the graph as "regression_ml.png".
You'll see that the best line is perhaps not a very good representation
of the data - the straight line isn't picking up the dip in the pattern
of the data at around a predictor value of 14, and it over-estimates at
that point pretty badly. We might be able to do better with a line that
has a quadratic effect included. We'll try that next, and then we'll use
the likelihoods of this model and the quadratic model to test whether
adding the quadratic has a statistically significant improvement in fit.
Hypothesis testing with likelihood - comparing two nested models with a likelihood ratio test
We are now going to do another maximum likelihood fit for a line to the same data, but this time we'll allow the data to have a quadratic curve in it.
The app below has a data graph to the left and a likelihood function graph to the right, just like the other examples. The data graph is identical (for the moment) to the regression data graph, but it is set up to allow you to include a quadratic term in the model. The model we're using is just y = Intercept + Slope (x) + Quad. term (x2), which will allow us to account for the upward curve in the data.
Because the model likelihood now depends on three different parameters it was necessary to put each one on an axis in the 3D graph of the likelihood. Since that doesn't leave an axis to plot likelihood against, this version has a single point whose size and color is affected by the likelihood. Right now with a slope of 0, intercept of 8.75, and quad term of 0 the point is black and in the lower right corner of the graph. As you get your model closer to the maximum likelihood possible for a quadratic line the dot will get bigger and redder.
1. First, find the model that maximizes the likelihood function. This is done just like with the linear regression, but now with three values to fiddle with instead of two. The model is very sensitive to changes in the quad term, and it's a little tricky to find the best set of values. To help you, I put the maximum likelihood values in the middle of the scales for the likelihood graph on the right - the best values will be close to -1.5 for the slope, 16.7 for the intercept, and 0.07 for the quad term. Enter these as your starting values and you'll have a much easier time working your way to the ML values. The likelihood of the model at its ML values is 2.74 e-4, get as close as you can to this value by fiddling with the slope, intercept, and quad term.
|
Slope: Intercept: Quad. term: |
|
I don't give you the choice of switching between likelihood, log likelihood, and negative log likelihood in this version of the app because it wouldn't really change the appearance of the dot on the likelihood function graph. But, if you hover over the point on the graph you'll see that these values are all reported for the currently selected slope, intercept, and quad term.
Click on the camera icon and download the graph for your ML quadratic regression model to your project folder - call it regression_quad_ml.png.
2. We now have two different models, and the quad model at least appears to fit the data better than the straight line. Since we are using the same data set for both models, and the models are nested we can test this with a likelihood ratio test. Nested models are ones in which all the parameters for the simpler model are also found in the more complex model - that is, the simpler model has a subset of the parameters in the more complex model. All we need are the model likelihoods, and the difference in degrees of freedom for the two models. The only difference between the two models is that the quad model has one more parameter, so the difference in degrees of freedom between them will be 1.
The likelihood ratio test uses twice the difference between the two log likelihoods as its test statistic (called G). This G statistic follows the Chi-square distribution, so to get a p-value we compare our G value to a Chi-square distribution with 1 degrees of freedom.
The calculations are done here - enter the log likelihood for your ML regression model (simpler), and your ML quadratic regression (more complex) in the entry boxes below (include the minus sign!). The p-value is calculated when you enter the values.
|
First model log likelihood: |
(the simpler model) |
|
|
Second model log likelihood: |
(the more complex model) |
|
|
Degrees of freedom: |
(difference in df for the two models) |
|
|
G statistic = |
|
(2 (log likelihood of first model - log likelihood of second model)) |
|
p-value = |
|
|
The more complex model will always fit the data at least a little better when the models are nested, so if p is less than 0.05 we can conclude that adding the quadratic term had a statistically significant improvement in model fit. You can also think of this as a test of the term that is included in one model but not the other, which is the quadratic term.
Record the results of this likelihood ratio test in your Rmd file.
Is the best-supported hypothesis any good at all?
Note that our likelihood ratio test gave us a comparison of two models: simple linear regression and quadratic regression. In this case we found that the quadratic regression fit better than the simple linear regression, but we don't get a test of the linear regression model. As we move into model-based inference we don't want to give up one very nice feature of null hypothesis testing - namely, the null hypothesis is the hypothesis of no effect, and we would like to know if we have any reason to think our predictors have any effect on the response at all.
.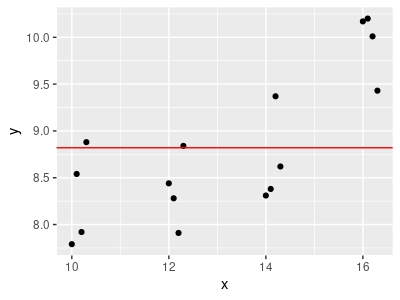
A model-based approach to testing a null hypothesis is to fit an intercept only model to the data and compare it to the linear regression model. A model that only has an intercept hypothesizes no relationship between y and x at all - or, if you prefer, it hypothesizes a flat line with a slope of 0 and an intercept at ȳ, like the graph on the left.
We can calculate the likelihood of the intercept-only model given the data the same way that we calculated the log likelihood of this model by going back up to the linear regression app and setting the intercept to the mean of the Y data (8.82), and the slope to 0, and selecting log likelihood from the drop-down menu. Since the intercept-only model has a subset of the terms that the regression model has, we can compare them with a likelihood ratio test to see if the regression model has a significantly higher likelihood. Enter the log likelihood of the intercept only model as the simpler model, and the linear regression log likelihood as the more complex model. Since the only difference between them is the slope of the linear regression there is still only 1 DF for the test. You should see that the linear regression fits statistically significantly better than a flat line.
Okay, that was fun - now we're going to do this set of regressions in R to see how this is really done. We'll come back for one more app at the end, but it's a bit of a departure from what we've been doing, so we'll save it for the end, like dessert.
Using R for likelihood ratio testing
R doesn't provide nice interactive illustrations to explain how it's doing what it's doing, but to do real work you would use R. Likelihood ratio tests comparing models are simple to do in R, using our familiar lm() model fitting.
1. Import the Regression sheet from likelihood_data.xlsx into an object called regression.
2. Fit a linear regression of y as the response against x as the predictor, and store the output in linear.lm. To see the coefficients put the name of the object, linear.lm, in the next row after the model is fitted - you should see they are very similar to what you got with the apps (these are of course better estimates, the apps above are pretty crude, but they should be close). Do this step in chunk linear.regression of your Rmd file.
3. Get the log likelihood for the linear.lm model (in chunk linear.regression.loglike of your Rmd file);
logLik(linear.lm)
You should get a value of -11.24156 with 3 degrees of freedom. This should be close to the value you got in the app. Note that the linear model has 3 degrees of freedom, because it estimated the slope, the intercept, and the standard deviation of the residuals. To simplify the examples I estimated the standard deviation of the residuals separately (cheated a little, forgive me - if we had included the standard deviation in the estimate those normal individual likelihoods could get broader or narrower).
4. Now fit the model with the quadratic term. The syntax is a little different, because R gets confused if you use the same predictor twice in a model formula - we need to use the identity function, I(), to get it to actually use the quadratic predictor. Put this in the quad.regression chunk of your Rmd file:
lm(y ~ x + I(x^2), data = regression) -> quad.lm
quad.lm
The coefficients should again be fairly close matches with what you got from the app.
You can get the log likelihood for this model in chunk quad.regression.loglike of your Rmd file. R's log likelihood should be close to what we got with the app.
This model has 5 df - one more than the linear regression model because of the quadratic term.
5. Fit the intercept only model in chunk intercept.only of your Rmd file:
lm(y ~ 1, data = regression) -> intercept.lm
intercept.lm
Using a 1 as a predictor with no variables fits an intercept-only model. You'll see that only an intercept coefficient is reported, and it is equal to the mean of the y data.
Get the log likelihood for this intercept only model in chunk int.only.log.likelihood. The log likelihood of the intercept-only model is quite a bit smaller than the other two - having no predictors in the model seems to lead to substantially lower likelihood.
6. Now to do the likelihood ratio tests. There is an lrtest() function in the lmtest library that does the test and gives output as we saw it in the app, above. To use it, in chunk likelihood.ratio.tests, enter:
library(lmtest)
lrtest(intercept.lm, regression.lm, quad.lm)
You'll see you get the following output:
Likelihood ratio test
Model 1: y ~ 1
Model 2: y ~ x
Model 3: y ~ x + I(x^2)
#Df LogLik Df Chisq
Pr(>Chisq)
1 2
-18.5567
2 3 -11.2416 1 14.6303 0.0001308 ***
3 4 -8.1878 1 6.1076 0.0134604
*
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Each row is a model, in the order you entered them into the lrtest() command. Models are compared to the model in the previous row, so the second row compares the linear regression to the intercept only model, and the third row compares the quadratic regression to the linear regression. We get significantly better fits by using x as a predictor than with no predictor at all, and by including a quadratic term over only using a linear regression. The results are very similar to what we got with the app, above.
You can also use the anova() command to get a similar test - instead of calculating the log likelihoods directly R calculates the residual sums of squares for each model and then uses those to calculate an approximate Chi-square test statistic for the comparisons. There's nothing wrong with using the lrtest() command, but just to see how the base R function output looks, enter (in the same chunk):
anova(intercept.lm, regression.lm, quad.lm, test = "Chisq")
and you'll see:
Analysis of Variance Table
Model 1: y ~ 1
Model 2: y ~ x
Model 3: y ~ x + I(x^2)
Res.Df RSS Df Sum of Sq
Pr(>Chi)
1 15
9.5286
2 14 3.8187 1 5.7100
9.498e-08 ***
3 13 2.6070 1
1.2117 0.01397 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
The results are very similar, but I prefer the lrtest() version - it reports the model log likelihoods, and uses those to calculate the G statistics used in the tests.
So, as you can see, R has good support for fitting models and comparing them. We'll make good use of this as we learn to use model-based analysis to compare hypotheses that don't include nested sets of predictors.
Likelihood of proportions, and profile likelihood confidence intervals
Proportions are commonly encountered in Biology, and are very simple quantities to calculate. If we had a sample of 20 individuals, of which 15 were heterozygous for a trait we were interested in, we could calculate the proportion that are heterozygous by dividing the number of heterozygotes by the total number observed, or p = 15/20 = 0.75 (don't confuse this for a p-value from a hypothesis test, we are using p to represent the proportion of heterozygotes for this example). Expressing the data as a proportion allows us to compare between samples with different numbers of individuals, and they are very simple, common values to work with.
But, just like a sample mean, the proportion of heterozygotes in a sample is a sample-based estimate of a population parameter. We might like to know, given that we have 15 heterozygotes out of 20 sampled, what range of possible proportion of heterozygotes in the population is likely given the data we have. In other words, we would like to be able to attach a confidence interval to this value of p.
This is a simple enough thing to want, but a surprisingly difficult thing to have. The way we calculate confidence intervals for sample means is to calculate a measure of sampling variation (the standard error), multiply it by a t-value that will capture 95% of the possible sample means from the population, multiply them together to get a measure of uncertainty (t x se), and then add the uncertainty to, and subtract it from, the mean. For a proportion the formulas are a little different, starting with the formula for the variance - with a proportion, p, the variance is:
σ2p = p(1-p)
The standard error is thus:
s.e.p =√p(1-p)/n
With a proportion of 0.75 and a sample size of 20 the standard error is √0.75(0.25)/20 = 0.097
With proportions we don't need to use the t-distribution, we can use the normal distribution in our confidence interval calculation - since 95% of a normal distribution falls between -1.96 and 1.96, we use 1.96 as the multiplier to calculate the uncertainty. We then add and subtract the uncertainty from p to get our 95% confidence interval:
0.75 ± 1.96 (0.097) = 0.56 to 0.94
Seems to work, right? There are some limitations to this approach though. First, the interval is obtained by adding and subtracting the same number to p, which gives us symmetrical confidence intervals. Given that the we can't get proportions lower than 0 or higher than 1 we should have a greater chance of the proportion falling below 0.75 than above it. We can see the problem even more clearly if we calculate the interval for a proportion closer to 1, like 0.9:
0.9 ± 1.96 √0.75(0.25)/20 = 0.77 to 1.03
Given that it isn't possible for a proportion to fall above 1 it's clear nonsense to suppose that it's possible for p to fall between 1 and 1.03. We're fortunate when the answers we get are nonsense, because we can recognize the error - it is still problematic to have symmetrical confidence intervals with p = 0.75, but the answers are plausible so the problem is less obvious then.
There are various ways to solve this problem that use the same basic approach with an adjustment to make the intervals symmetrical and force them to stay between 0 and 1, but none are based on a simple understanding of the uncertainty involved, and not very statistically elegant (if that's the kind of thing you worry about).
A better solution is to use the likelihood function to obtain our confidence intervals. It can be shown that the two values for the parameter whose likelihoods are 1.92 units below the maximum log likelihood are good estimates for the lower and upper 95% confidence interval. This sounds complicated, but once you have the likelihood function it really isn't. We'll try it out with our proportion of heterozygotes example below.
The likelihood function for a proportion is simple - it's pn(1-p)K-n, where p is the proportion of heterozygotes, n is the number of heterozygotes, (1-p) is the proportion of not heterozygotes (i.e. the homozygotes), and K - n is the number of not heterozygotes (K is the total individuals, n is the number of heterozygotes, so K - n is the number of homozygotes). The likelihood function for a range of possible values of p is shown in the graph to the right.
1. The app is set to 15 heterozygotes out of 20, which is a proportion of 0.75. The current estimate for the value of p is selected by the slider, which begins at 0.5. It's convenient to think of proportions as the balancing points for count data - the graph on the left shows bars for homozygotes and heterozygotes, and you can think of the x-axis as a teeter-totter. The current value of 0.5 is in the middle of the teeter totter, and it's unbalanced - the greater number of heterozygotes are weighing down the right side and making the graph tilt. If you move the slider to the right you'll see that you get the graph balanced at p = 0.75, which is also the maximum likelihood estimate according to the graph on the right.
Number sampled:
Number of heterozygotes:
2. With the slider set at 0.75 change the type of likelihood to log likelihood. You'll see that the log likelihood has a much flatter top, but it does have a maximum value, and it's the same place as the peak of the likelihood function. If you hover over the red dot you'll see that the log likelihood for p = 0.75 is -11.2467. The values that are 1.92 units below that will be at a log likelihood of -11.2467 - 1.92 = -13.1667. If you move your mouse along the likelihood function to the left until you find a value of -13.12544 (the closest my app will let you get to -13.1667) at p = 0.54 (you can see the value for p in a little black text box that pops up below the x-axis) - this is the lower limit for the 95% confidence interval.
If you do the same thing above 0.75, you will find the value of -13.09333 (which is the closest the app gets to -13.1667 on the upper end of the curve) at p = 0.9, which is the upper limit.
So, according to our likelihood function, given our ML estimate of p = 0.75 we can have 95% confidence that the true value falls between 0.54 and 0.9. Because the likelihood function is not symmetrical this method gives us asymmetrical intervals. And, because the likelihood function is bounded at 0 and 1 we can't get ridiculous values as our limits, like values below 0 or above 1.
3. Change the number of heterozygotes to 4, keeping the total at 20, which is a p of 4/20 = 0.2. Set the slider to 0.2, and confirm you're at the maximum likelihood estimate. Then, find the log likelihood at p = 0.2, calculate the value that is 1.92 units below this maximum value, and then find the lower and upper limits. Report these in your Rmd file.
4. We would expect that adding more data would give us narrower confidence intervals. We can confirm this happens by setting the total to 100 and the number of heterozygotes to 20 - this also gives us a p of 20/100 = 0.2. If you do your profile likelihood with this larger data set you'll find the log likelihood is much more curved around the estimate, and it gives us a narrower confidence interval as a result. Report the confidence interval for this larger sample size in your Rmd file.
This method of using the likelihood function to find a confidence interval is called profiling the likelihood function, and the interval is a profile likelihood confidence interval.
That's it! Knit and upload your Word document.