We will be working today with an approach to statistical inference based on comparisons of likelihoods among models, rather than on null hypothesis tests. With this approach each model is treated as a hypothesis about the structure of the data, and we seek to find which hypothesis is best supported by the data. This approach is called the method of support.
Our approach throughout all but the last couple of weeks of the semester has been to test a single null hypothesis. With a null hypothesis test we assume the null is true, calculate the probability of obtaining our results if the null is true, and if the probability is low we reject the null in favor of an unspecified alternative hypothesis. This procedure seems to set up a competition between two different hypotheses, the null and the alternative, but these two hypotheses are conceptually very different. The null hypothesis says that there is exactly 0 difference between group means (or that the slope of a regression line is exactly 0), whereas the alternative hypothesis is just that the null is incorrect. When we reject the null we may have reason to think that a difference of 0 is not well supported by the data, but we have not done anything to evaluate the support for any other amount of difference specifically - treating evidence against one hypothesis as though it's evidence for another is a logical fallacy called a false dichotomy.
The method of support is very different. With the method of support it isn't possible to test a single hypothesis alone, like we do with a null hypothesis, because we can't draw any conclusions at all from a single model. Instead, we need to compare models to one another to draw any conclusions.
There are several important points to bear in mind about the method of support:
-
It is model based, which means that we have to be able to express our hypotheses as models. For example, we learned in our classic model selection exercise that:
-
If a predictor variable is included in the model, we are hypothesizing that the response depends on it. Conversely, if a predictor is excluded, we are hypothesizing that the response is independent of it.
-
If we combine two or more levels of a categorical grouping variable together, we are hypothesizing that the two different levels have the same mean. If we split a single level into two or more different levels, we are hypothesizing that each new level has a different mean.
-
If we include a quadratic, cubic, or other higher-order term for a predictor, we are hypothesizing that the response has this specific non-linear relationship with the predictor.
-
If we include an interaction between two predictors we are hypothesizing that the response to one predictor depends on the level of the other.
-
-
Support for hypotheses is assessed at the level of the model. To assess the importance of a specific variable, or a model term (such as an interaction) you must fit models that include the the variable/term and others that do not, and assess which model is best supported by the data.
-
Model-based inference only works if the same response data are used for every model. Any set of predictors can be included, and models can be compared even if they contain completely different sets of predictors. Specific cases that would be problematic are:
-
A missing value from one of the predictor variables causes R to drop the entire row of data from the analysis, including the response variable's data value. If some models use the entire data set and others are missing a data point or two, you shouldn't compare the models.
-
The response variable needs to be on the same scale for all of the models - you can use an untransformed response variable for every model, or a transformed response variable for every model, but they all must be the same. You can, however, transform only some of your predictors, and can even compare a model with a transformed predictor to one with the un-transformed version of the same predictor as two separate hypotheses.
-
-
We have to assume a distribution of residuals around the model to calculate likelihoods and AIC values, so we should assess the usual GLM assumptions for any model we wish to interpret. Models that are poorly supported that don't meet GLM assumptions are not a problem, but any model that is well enough supported that we wish to interpret it should meet GLM assumptions.
- The end result of this approach is not a "test" of a hypothesis in the sense that there is no binary pass/fail decision made about the hypothesis. Measures of support for hypotheses, such as AIC's and model weights, are meant as relative measures, which we should use to gauge the strength of our confidence in our conclusions.
-
Measures of support do not substitute for measures of model fit or effect size, such as R2, because the best-supported model in the set we are considering could still be lousy. We should also always include an "intercept only" model to check the "no effect" hypothesis - only models that are better supported than the "no effect" model should be considered for interpretation.
Although this method can be used to analyze any data set, it is most attractive for studies in which the null hypothesis is not plausible. As we discussed in lecture, this covers nearly all ecological studies, and any lab study in which random allocation of subjects to treatments is not possible.
Today's exercise - the brain/body size relationship
This exercise will be based on brain weight and body weight for a variety of species of animals. Most are mammals, but there are three dinosaurs included (their weights are estimated values, based on the sizes of their skeletons).
Start a new R Studio project in a new folder. The data set we will use today is here, and the Rmd file is here. Import the data into a dataset called "brains".
If you look at the way the data are organized you will see that it contains data on the log of brain mass, the log of body mass, the identity of the species (Species column), and four different hypothetical groupings of the species:
1) dinosaurs separate from mammals, mammals grouped by Order (column Taxa)
2) dinosaurs separated from non-dinosaurs (column Dino.nodino)
3) primates separated from non-primates (column Primate.noprimate)
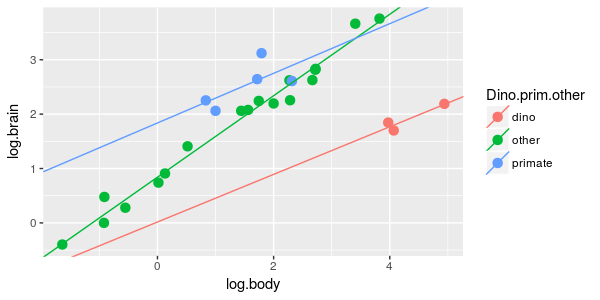
4) dinosaurs, primates, and other mammal species (column Dino.prim.other)
|
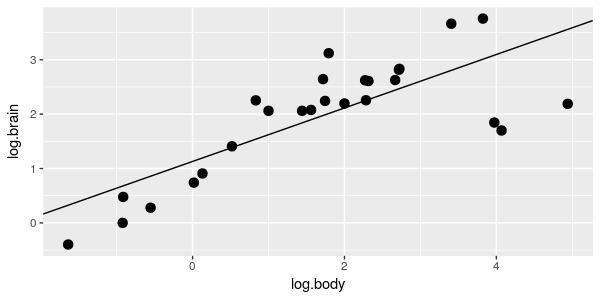
You can see that there is a general, positive relationship between body size and brain size, which makes sense - a large part of the mass of the brain is devoted to simply operating the body, and large bodies require large brains to operate them. |
|
|
For this exercise, we are interested in finding a model that best represents the brain size/body size relationships of these species. To give you an idea of how this will work, let's look at a couple of examples of hypotheses we could evaluate. |
|
|
The AICc value for this model is -16.89. |
|
|
It certainly looks like a separate line is desirable for the dinosaurs, and not surprisingly the AICc for this model of -57.21 is substantially lower than for the single line hypothesis above. This model is the better of the two we have looked at so far, and if we subtract the AICc for this model from each of the first two, we would get a ΔAICc of 0 for this model, and 40.31 for the single line model. With just these first two models to consider, the simple linear regression can be safely disregarded in favor of this ANCOVA model. |
|
|
This model also looks pretty good, but we had to add an additional parameter to produce the differences in slope. The AICc value for this model is -56.98, not quite as small as the previous one. The previous model with parallel lines is still best supported (with a ΔAICc of 0), and this model with different slopes has a ΔAICc is 2.13. |
|
With just these three models to go on we could confidently conclude that dinosaurs and mammals are different enough to need their own lines (ΔAICc is huge for the model with a single line), but whether their scaling relationships have the same slope or different slopes is less certain (ΔAICc = 2.13 for the model that includes an interaction between log body weight and dino.nodino).
We will implement these three models, and six more that use the other grouping variables in the data set to determine which hypotheses are well supported by the data, and which are poorly supported.
Instructions:
1. We will fit several models to compare, and need to collect them all in a list, just like we did when we were using adjusted R2 to analyze caloric content of foods. To start, we will create an empty list into which we can add our fitted models. Use the command (in the make.models.list of your Rmd file):
models.list <- list()
Now each time we fit a model we will add it as a named element of our models.list object.
For example, the hypothesis that there is a single brain/body scaling relationship for all of these species is a simple linear regression of log.brain on log.body (in the log.brain.on.log.body chunk of your Rmd file):
models.list$body.lm <- lm(log.brain~log.body, data = brains)
By assigning the output of the lm() statement to models.list$body.lm we create a named element called body.lm within the models.list object, and store the fitted model within it.
That takes care of the first hypothesis' model, out of a total of 10 hypotheses we will compare. Since the method of support uses models to represent hypotheses, the translation of scientific hypothesis first to a type of linear model, and then to an R model formula to use in the lm() function, is shown for each hypothesis in the table below. It is structured like so:
- The scientific hypothesis is stated first, expressed in scientific terms, in the "Scientific hypothesis" column
- The hypothesis is then translated into the type of linear model that would be used to represent the hypothetical relationship between variables stated in the Scientific hypothesis column. If you hover over the "Hypothesis as a linear model" for a hypothesis a graph pops up to show what the lm will look like
- The model formula you will use in R to represent the model is shown next, in the "R model formula" column. The model formula to use is displayed for the first two models (the first one being the body.lm model you already assigned to models.list). For the third to tenth model the model formula is hidden until you click "What is the model?" - take a moment to construct the model formula yourself before looking at the answer, it will give you useful practice for when you have to do this on your own
- The name of the model to use when you assign the lm to models.list is given last, in the "Name of model to use" column. The model name aren't critical, but the rest of the instructions will be easier to interpret if you stick with these names
Go ahead and fit the 2nd through 10th models, adding each to your models.list (in the fit.remaining.models chunk of the Rmd file).
| Scientific hypothesis | Hypothesis as a linear model (hover for graph) | R model formula: | Name of model to use |
|---|---|---|---|
| 1. There is a single common brain/body scaling relationship for all species in the set. |
Simple linear regression of log.brain on log.body
 |
log.brain ~ log.body |
body.lm |
| 2. The scaling of brain size and body size is the same for all species, but taxa differ in their average brain sizes for their body size. |
ANCOVA of log.brain by taxa, with log.body as a covariate
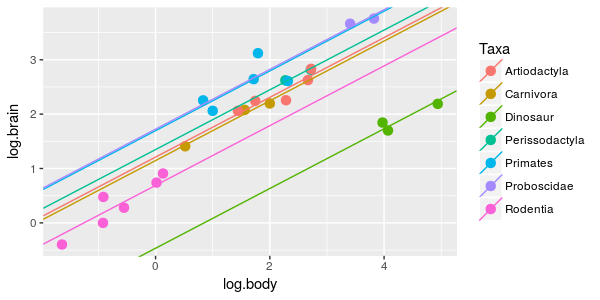 |
log.brain ~ log.body + Taxa |
taxa.lm |
| 3. Each taxa has a different scaling relationship. |
ANCOVA of log.brain on taxa and log.body, with an interaction between log.body and
taxa.
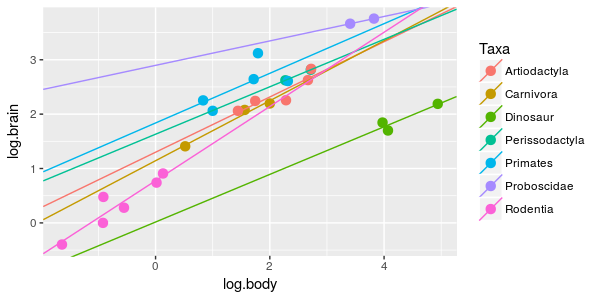 |
What is the model? | taxa.int.lm |
| 4. Brain/body scaling is the same for dinosaurs and non-dinosaurs, but with different averages between the groups. |
ANCOVA of log.brain by dino.nodino, with log.body as a covariate
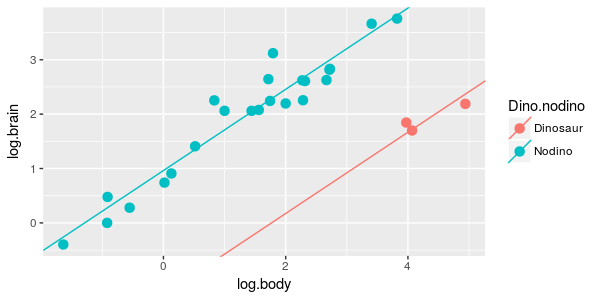 |
What is the model? | dino.lm |
| 5. Brain/body scaling is different for dinosaurs and non-dinosaurs. |
ANCOVA of log.brain on dino.nodino and log.body, with an interaction between
dino.nodino and log.body
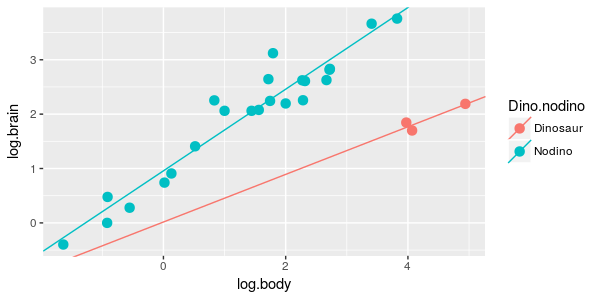 |
What is the model? | dino.int.lm |
| 6. Brain/body scaling is the same for primates and non-primates, but with different averages between the
groups. |
ANCOVA of log.brain by primate.noprimate, with log.body as a covariate
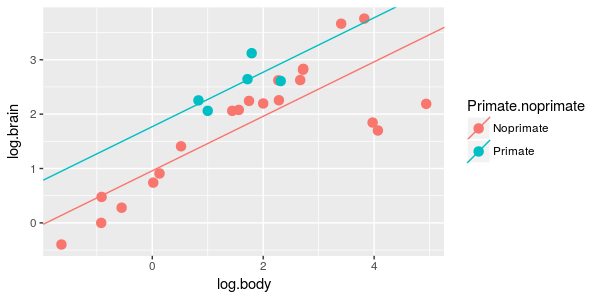 |
What is the model? | primate.lm |
| 7. Brain/body scaling is different for primates and non-primates. |
ANCOVA of log.brain on primate.noprimate and log.body, with an interaction between
primate.noprimate and log.body
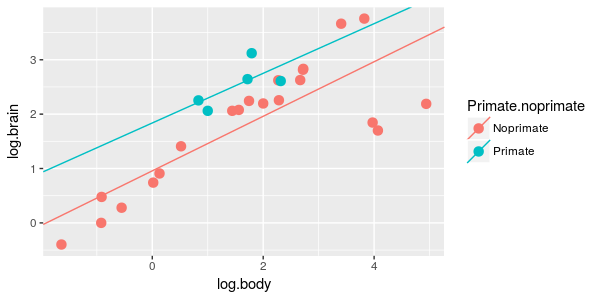 |
What is the model? | primate.int.lm |
| 8. Brain/body scaling is the same for dinosaurs, primates, and other mammal, but with different averages
between the groups. |
ANCOVA of log.brain by dino.prim.other, with log.body as a covariate
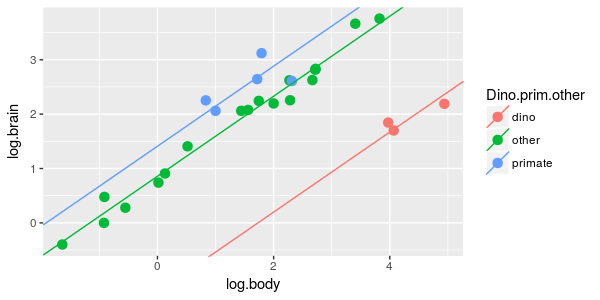 |
What is the model? | dpo.lm |
| 9. Brain/body scaling is different for dinosaurs, primates, and other mammals. |
ANCOVA of log.brain on dino.prim.other and log.body, with an interaction between
dino.prim.other and log.body
 |
What is the model? | dpo.int.lm |
| 10. There is no predictable relationship between brain size and body size for these species. In other
words, brain size is independent of body size. |
The "intercept only" model.
 |
log.brain ~ 1 | intercept.only.lm |
When you're done you can check the names in your list (in the show.model.list.elements chunk of
the Rmd file):
names(models.list)
You should see the names:
[1] "body.lm"
"taxa.lm"
"taxa.int.lm"
"dino.lm"
[5] "dino.int.lm" "primate.lm"
"primate.int.lm" "dpo.lm"
[9] "dpo.int.lm" "intercept.only.lm"
If you don't see this list of names, read the blockquote section for instructions for fixing errors.
IF YOU MAKE A MISTAKE read this for the fix (otherwise skip to step 2 below).
- If you made a mistake in the model statement, but used the correct model name, edit the command and assign the correct model to the same named list element. The mistake will be replaced by the corrected model.
- If you use the right model statement but used the wrong model name, you can change the name if you know the number of the model. Look at the number of the named elements, and find the number for the incorrect one. For example, if you were to get names like:
[1] "boody.lm" "taxa.lm" "taxa.int.lm" "dino.lm"
[5] "dino.int.lm" "primate.lm" "primate.int.lm" "dpo.lm"
[9] "dpo.int.lm" "intercept.only.lm"
The incorrect name is the first in the list, which has index number 1. You can change its name with:
names(models.list)[1] <- "body.lm"
This will replace the wrong name with the right one.- If you accidentally included a model that you don't want, use the command:
models.list$mistake.name <- NULL
This will delete the model from the list.
2. After you have added all 10 models to models.list you need to extract their AIC values for analysis. We can use sapply() for this, using R's extractAIC() function applied to each of the named models in models.list. The extractAIC() function extracts AIC and number of parameters from a fitted model. Try it out in the Console on the first model, body.lm, with the command (in the console):
extractAIC(models.list$body.lm)
You will get two values, the first being the number of parameters in the model (2, which is K in the AIC formula), and AIC (which is -17.36706 for this model).
We can use extractAIC() as the function in an sapply() command, which will extract K and AIC for each model in models.list. The command is (in the Console):
sapply(models.list, extractAIC)
which gives you this:
body.lm taxa.lm taxa.int.lm dino.lm
dino.int.lm primate.lm primate.int.lm dpo.lm
[1,] 2.00000 8.00000 14.00000
3.00000 4.00000
3.00000 4.0000 4.00000
[2,] -17.36705 -79.14906 -70.07542 -58.16365 -56.81901
-22.22915 -20.2379 -76.33646
dpo.int.lm intercept.only.lm
[1,] 6.000 1.000000
[2,] -77.238 4.424834
This command gives us the information that we want, but it's in the wrong orientation - each model is a column instead of a row, and our numbers of parameters and AIC's are rows instead of columns. Fortunately, swapping rows and columns is a simple matrix operation called "transposition". We can transpose the matrix using the t() command (in the Console):
t(sapply(models.list, extractAIC))
which gives us:
[,1] [,2]
body.lm 2 -17.367054
taxa.lm 8 -79.149058
taxa.int.lm 14 -70.075416
dino.lm 3 -58.163652
dino.int.lm 4 -56.819013
primate.lm 3 -22.229149
primate.int.lm 4 -20.237899
dpo.lm 4 -76.336462
dpo.int.lm 6 -77.237999
intercept.only.lm 1 4.424834
This output has the orientation we want, so we're almost there. At this point the output is still a matrix rather than a data frame, which we can fix by wrapping our t(sapply()) inside of a data.frame() command, like so (put this version into the extract.aic chunk of your Rmd file):
model.aic <- data.frame(t(sapply(models.list, extractAIC)))
If you type model.aic you'll see you now have the data organized as we want, but without informative column names. We can add column names to the model.aic data frame with (in the rename.k.and.aic.columns chunk of your Rmd file):
colnames(model.aic) <- c("K","AIC")
The final version of the table, with column labels, looks like this:
K AIC
body.lm 2 -17.367054
taxa.lm 8 -79.149058
taxa.int.lm 14 -70.075416
dino.lm 3 -58.163652
dino.int.lm 4 -56.819013
primate.lm 3 -22.229149
primate.int.lm 4 -20.237899
dpo.lm 4 -76.336462
dpo.int.lm 6 -77.237999
intercept.only.lm 1 4.424834
The list of model names on the left are row names for the data frame rather than a column of data, so they do not have a column name.
3. Now that we have K and AIC for each model in our model.aic data frame, we can calculate AICc. AICc is just AIC plus an additional penalty for each model parameter, equal to 2k(k+1)/(n-k-1). k will come from the K column of model.aic, and n is the sample size (which is 26 for this data set).
The calculation is thus (in the calculate.AICc chunk of your Rmd file):
model.aic$AICc <- with(model.aic, AIC + 2*K*(K+1)/(26-K-1))
If you type model.aic, you'll see there is now a column called AICc with the results of these calculations.
4. We can now calculate delta AIC values, which are much easier to interpret than the raw AICc values. The command is (in the calculate.delta.AICc chunk of the Rmd file):
model.aic$dAICc <- model.aic$AICc - min(model.aic$AICc)
This command takes the AICc's we just calculated and subtracts the smallest AICc from each of them. Type model.aic in the console and you'll see:
K AIC AICc
dAICc
body.lm 2 -17.367054 -16.845315 57.586385
taxa.lm 8 -79.149058 -70.678470 3.753230
taxa.int.lm 14 -70.075416 -31.893598 42.538102
dino.lm 3 -58.163652 -57.072743 17.358957
dino.int.lm 4 -56.819013 -54.914251 19.517449
primate.lm 3 -22.229149 -21.138240 53.293460
primate.int.lm 4 -20.237899 -18.333137 56.098563
dpo.lm 4 -76.336462 -74.431700
0.000000
dpo.int.lm 6 -77.237999 -72.816947 1.614753
intercept.only.lm 1 4.424834 4.591501 79.023201
The model with the smallest AICc has a dAICc of zero, and the rest are differences from this model's AICc.
5. Finally, let's calculate the Akaike weights. Remember, these are measures of how often we would expect the model to be best-supported if we repeated the exercise with new data; they are useful for attaching a more intuitive interpretation of degree of support for the models than we get from the ΔAICc values alone. These are calculated with (in the calculate.AICc.weights chunk of your Rmd file):
model.aic$wts <- with(model.aic, exp(-0.5*dAICc)/sum(exp(-0.5*dAICc)))
This calculation divides each model's exp(-0.5*dAICc) by the sum of the exp(-0.5*dAICc) for all of the models. Since we're dividing each model's value by a total across all of the models, these values are proportions - they must fall between 0 and 1, and sum to 1 across the models.
6. Traditionally, tables of AIC statistics are sorted on dAICc to make it easier to see which models are best supported. We're going to use the order() command to give the rank order of the dAICc values - in the console write:
order(model.aic$dAICc)
and you will get:
[1] 8 9 2 4 5 3 6 7 1 10
After the index, [1], the numbers are the row numbers from dAICc - the eight row is the smallest dAICc, the ninth is the second smallest dAICc, and so on. We can use these numbers to sort the entire model.aic data frame if we use them as the row index - do so with this command (in the console):
model.aic[order(model.aic$dAICc), ]
which gives you:
K AIC AICc
dAICc wts
dpo.lm 4 -76.336462 -74.431700
0.000000 6.252494e-01
dpo.int.lm 6 -77.237999 -72.816947 1.614753 2.788778e-01
taxa.lm 8 -79.149058 -70.678470 3.753230
9.573036e-02
dino.lm 3 -58.163652 -57.072743 17.358957
1.063172e-04
dino.int.lm 4 -56.819013 -54.914251 19.517449 3.613209e-05
taxa.int.lm 14 -70.075416 -31.893598 42.538102 3.622611e-10
primate.lm 3 -22.229149 -21.138240 53.293460 1.673113e-12
primate.int.lm 4 -20.237899 -18.333137 56.098563 4.115334e-13
body.lm 2 -17.367054 -16.845315 57.586385
1.955819e-13
intercept.only.lm 1 4.424834 4.591501 79.023201 4.328956e-18
This command put the row numbers from the order() command into the row index position for model.aic, which puts the model.aic data in order by the dAICc column.
We can compare the weights more easily if we suppress the scientific notation - use the command (in your Rmd file, sort.and.display.output chunk):
format(model.aic[order(model.aic$dAICc),], digits = 2, scientific = F)
which gives you:
K AIC AICc
dAICc
wts
dpo.lm 4 -76.3 -74.4 0.0
0.6252493597029067374
dpo.int.lm 6 -77.2 -72.8 1.6 0.2788778324035202094
taxa.lm 8 -79.1 -70.7 3.8
0.0957303581929313807
dino.lm 3 -58.2 -57.1 17.4
0.0001063172432656724
dino.int.lm 4 -56.8 -54.9 19.5 0.0000361320928347135
taxa.int.lm 14 -70.1 -31.9 42.5 0.0000000003622611060
primate.lm 3 -22.2 -21.1 53.3 0.0000000000016731133
primate.int.lm 4 -20.2 -18.3 56.1 0.0000000000004115334
body.lm 2 -17.4 -16.8 57.6
0.0000000000001955819
intercept.only.lm 1 4.4 4.6 79.0 0.0000000000000000043
As you interpret this table, remember:
- The best-supported model has the lowest AICc, and will have a dAICc of 0
- dAICc values below 2 are considered more or less equivalent models - they are both well supported by the data, and the data provides little basis for preferring one over the other
- dAICc values of 4 to 10 indicate substantially lower support than the best supported model
- dAICc values over 10 are sufficiently large that the models can be disregarded
You should see that the weight is biggest for the model with a dAICc of 0, but for models with dAICc's less than 4 the weights are still fairly high. The weights indicate the relative frequency with which we would expect the model to be best if we collected a new data set. Based on these weights we can be confident that some hypotheses are very poorly supported by the data (intercept.only.lm, body.lm, and the other models with dAICc above 10), but there are three with dAICc values less than 4 (taxa.lm, dpo.int.lm, and dpo.lm), one of which has a dAICc of only 1.6. With these data we have weak support for interpreting just the bet-supported model, and should consider dpo.int.lm as fairly equivalent to dpo.lm. The taxa.lm model has substantially less support than either dpo.int.lm or dpo.lm, but with a weight slightly below 4 it cannot be completely discounted.
7. At this point we have information about how much support there is for each model in the data, but that's only the first step in data analysis. We can address how important individual variables are by summing the weights for the models each variable appears in. There are various ways of doing this, but the seemingly simplest method of calculating them by hand is error-prone, and it would be much better to take advantage of the fact that we already have the information we need in the models.list and model.aic objects. We just need to figure out how to get it in a form that can be used to calculate the weights by variable.
To do this calculation, we will:
- Make a data frame with variable names as columns, and model names as rows, with a 1 entered when a variable appears in a model, and a 0 when it does not
- Multiply the matrix of 0's and 1's by the model weights, and sum the columns
The data frame we want to make looks like this:
log.body taxa dino primate dpo
body.lm
1 0 0 0 0
taxa.lm
1 1 0 0 0
taxa.int.lm 1
1 0 0 0
dino.lm
1 0 1 0 0
dino.int.lm 1
0 1 0 0
primate.lm
1 0 0 1 0
primate.int.lm 1
0 0 1 0
dpo.lm
1 0 0 0 1
dpo.int.lm
1 0 0 0 1
intercept.only.lm 0 0
0 0 0
Each row is a model, and they are in the same order as they appear in models.list. Each column is the name of one of our predictor variables. If the variable appears in the model it gets a 1 for that row, and if the variable does not it gets a 0. If you look at the log.body column, there are 1's in each row except for intercept.only.lm, because log.body occurs in every model but the intercept only model. Reading across columns by row, the body.lm model had only log.body as a predictor, so there is a 1 for the log.body variable, and a 0 for the rest.
To make this table, we will make the columns as vectors, and then combine the columns together in a data frame. In the which.models.variables.are.in chunk of your Rmd file enter the first column:
log.body <- c(1,1,1,1,1,1,1,1,1,0)
We entered the values as a vector, so we had to enter them horizontally, but you'll see we have 9 1's in a row followed by a 0, which is the same as the log.body column.
To make taxa we need a 1 as the second and the third elements, and 0's for the other eight:
taxa <- c(0,1,1,0,0,0,0,0,0,0)
The dino variable appears in the fourth and fifth models, so we have:
dino <- c(0,0,0,1,1,0,0,0,0,0)
The primate variable is in the sixth and seventh models:
primate <- c(0,0,0,0,0,1,1,0,0,0)
And last, dpo is in the eighth and ninth models:
dpo <- c(0,0,0,0,0,0,0,1,1,0)
To combine these into a data frame we use (in the make.variable.inclusion.data.frame chunk of your Rmd file):
data.frame(log.body, taxa, dino, primate, dpo) -> variables.in.model
You can use the names of the models from models.list as the row names for this data frame (in the same chunk of your Rmd file):
row.names(variables.in.model) <- names(models.list)
If you then display the variables.in.model data frame you'll see we have the same table shown above - if you see any 1's in the wrong location go back and check your vectors to make sure they were all done correctly.
Now that we have the variables.in.model data frame, we can use it to select which model weights to include when calculating the importance for each variable. If we multiply the model weights by each column in the variables.in.matrix data frame, we'll get the weight everywhere we have a 1, and a 0 everywhere we have a 0. In the console type:
model.aic$wts * variables.in.model
to get:
log.body taxa
dino primate dpo
body.lm 1.955819e-13 0.000000e+00 0.000000e+00
0.000000e+00 0.0000000
taxa.lm 9.573036e-02 9.573036e-02 0.000000e+00
0.000000e+00 0.0000000
taxa.int.lm 3.622611e-10 3.622611e-10 0.000000e+00 0.000000e+00 0.0000000
dino.lm 1.063172e-04 0.000000e+00 1.063172e-04
0.000000e+00 0.0000000
dino.int.lm 3.613209e-05 0.000000e+00 3.613209e-05 0.000000e+00 0.0000000
primate.lm 1.673113e-12 0.000000e+00 0.000000e+00 1.673113e-12
0.0000000
primate.int.lm 4.115334e-13 0.000000e+00 0.000000e+00 4.115334e-13 0.0000000
dpo.lm 6.252494e-01 0.000000e+00 0.000000e+00
0.000000e+00 0.6252494
dpo.int.lm 2.788778e-01 0.000000e+00 0.000000e+00 0.000000e+00
0.2788778
intercept.only.lm 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.0000000
Each number in the output is now either the weight for the model, if a variable occurred in it, or a 0, if the variable did not occur in it. This means that every column has the weight for every model it occurs in, and we can just sum the columns to get a measure of how important the variable is.
To do this, change the last command to (in the console):
colSums(model.aic$wts * preds.by.model)
and you will see:
log.body
taxa dino
primate dpo
1.000000e+00 9.573036e-02 1.424493e-04 2.084647e-12 9.041272e-01
These values too fall between 0 and 1 - the closer to 1 they are the more important the variable is to include, and the better supported it is by the data.
These variable importance values are complete, but are a little hard to compare because of the scientific notation. So, for the final command for the calculate.variable.weights chunk of your Rmd file should use the format() command to suppress scientific notation:
format(colSums(model.aic$wts * variables.in.model), scientific = F)
you'll see:
log.body
Taxa Dino.nodino
Primate.noprimate Dino.prim.other
"1.000000000000000000" "0.095730358555192491" "0.000142449336100386" "0.000000000002084647"
"0.904127192106426891"
What can we learn from these? At the level of the models, we couldn't be too certain that the best model to explain the brain data was the one with Dino.prim.other and log.body without an interaction, because including an interaction between Dino,prim.other and log.body was also fairly well supported. However, based on these variable weights we can be very confident that Dino.prim.other and log.body are both very important - the sum of the weights for the nine models that include log.body is very close to 1, and the sum of the weights for the two models that include Dino.prim.other is 0.904. We may not be too certain of whether the slopes of the lines are the same or different, but the best grouping of the taxa to use is to separate dinosaurs and primates, but keep the rest of the species lumped together.
Taxa is interesting as a variable, because it separates all of the taxa - this means that it too separates primates and separates dinosaurs. Taxa differs from Dino.prim.other only in that it keeps all the mammal Orders separate that Dino.prim.other lumps together into the "Other" category. Since Taxa splits the groups that are also split in Dino.prim.other, its log likelihood has to be at least as big as Dino.prim.other, but the extra parameters needed to split the other mammal Orders evidently penalizes Taxa more than it gains in a higher log likelihood by including them. It may be that with a larger sample size that Taxa could be better supported, but at this sample size the trade-off between complexity and fit is working against Taxa, and because of this the data doesn't support interpreting differences among groups other than those used in Dino.prim.other.
Post-hocs from a Method of Support perspective
For the Method of Support to be a viable alternative to using a conventional approach, with null hypothesis significance testing and p-values, we need to be able to answer the questions we would normally ask with conventional methods. If we had only been interested in a typical ANCOVA analysis, in which we used Dino.prim.other as a grouping variable and log.body as a covariate, we would have run into the problem that we don't just want to know that Dino.prim.other is well supported - we also want to know which of the three groups are different from one another. Having found that Dino.prim.other is well supported as a variable, we wouldn't want to fall back on using Tukey tests, because those are based on null hypothesis testing. How could we find out which groups are different from which using the Method of Support?
The way to do it is to evaluate which groupings are best supported. When you find that groups are not different in a Tukey test, you conclude they are not actually two separate groups, so a model that lumps them together would be better supported than one that splits them apart. If we used different models that had species grouped in different ways, we could see which was best supported, and interpret that model - groups that were split apart are different, those that are lumped together are not, according to the best-supported model.
If you look at the graph for dpo.lm above, you'll see that primates have the biggest brains for their body sizes, followed by the non-primate mammals, followed by dinosaurs. Combining primates and dinosaurs together, but leaving the other mammals separate doesn't make sense because we would be combining the biggest and smallest brains together and leaving the medium-sized brains in their own group - we can leave this possibility out of the analysis (you could make a predictor that represents this grouping, but it isn't necessary). The groupings we would want to hypothesize would thus be:
- All three groups are the same
- Primates and mammals are together, separate from dinosaurs
- Mammals and dinosaurs are together, separate from primates
- All three groups are separate
To do post-hoc analysis on the Dino.prim.other variable we would have a model for each of these. As it happens, we already have them:
- All three groups are hypothesized to be the same by the body.lm model
- Dinosaurs are hypothesized to be different from all of the mammals, but the mammals are grouped together, in the dino.lm model
- Primates are separated, but the rest of the mammals and the dinosaurs are grouped in the primate.lm model
- All three are separate in the dpo.lm model
We can pull these out of model.aic (in the console):
model.aic[ c("body.lm","dino.lm","primate.lm","dpo.lm"),]
which gives you:
K AIC AICc dAICc wts
body.lm 2 -17.36705 -16.84531 57.58639 1.955819e-13
dino.lm 3 -58.16365 -57.07274 17.35896 1.063172e-04
primate.lm 3 -22.22915 -21.13824 53.29346 1.673113e-12
dpo.lm 4 -76.33646 -74.43170 0.00000 6.252494e-01Since the AIC and AICc calculations are done at the level of individual models they don't need to be re-calculated in this new table. dAICc would need to be re-calculated if the model with the lowest AICc wasn't included in the table, but dpo.lm is included - all of these dAICc numbers are differences from dpo.lm already, so they don't need to be updated. The weights are calculated from dAICc's for all ten of the models in model.aic, so these would need to be re-calculated to use them, but we don't need them here - we'll just look at the dAICc numbers.
Based on this table, the dpo.lm model that separates dino, primate, and other has much lower AICc than the next closest grouping, which is found in dino.lm. The dino.lm dAICc is -17.35, which is much larger than the 10 units considered sufficient to discount a hypothesis completely. Given this, separating all three groups in Dino.prim.other is far and away the best grouping, and we can take this as evidence that all three are different from one another.
So, from this you can see that it's possible to use the Method of Support to analyze data that we've used hypothesis tests for up until now.
The other question we would ask in a typical ANCOVA is about the covariate, log.body - how do we know that log.body is supported? We could include the intercept only model as well in our analysis:
model.aic[ c("intercept.only.lm", "body.lm","dino.lm","primate.lm","dpo.lm"),]
which shows us:
K AIC AICc dAICc wts
intercept.only.lm 1 4.424834 4.591501 79.02320 4.328956e-18
body.lm 2 -17.367054 -16.845315 57.58639 1.955819e-13
dino.lm 3 -58.163652 -57.072743 17.35896 1.063172e-04
primate.lm 3 -22.229149 -21.138240 53.29346 1.673113e-12
dpo.lm 4 -76.336462 -74.431700 0.00000 6.252494e-01The difference between the intercept.only.lm and body.lm is about 22 units, so we have excellent reason to conclude there is a relationship between brain size and body size as well.
Note too that this approach puts the null hypothesis on the same footing as the hypotheses of a relationship between predictors and response - rather than testing the null and then treating a conclusion of "not the null" as though it is support for a particular relationship between variables, we treat the hypothesis of no relationship between the variables the same as the hypotheses of various affirmative relationships between variables, and then let the data tell us which is best supported. This gets away from the false dichotomies of null hypothesis testing, while letting us retain the hypothesis of no relationship whatsoever in our analysis.
Note one more quirk of the way that I've designed this analysis - log.body is in every model except for the intercept only model. Not surprisingly, its importance is near 1, because we haven't really made it compete against other hypotheses in which is was omitted. If we seriously thought that there might not be a relationship between brain size and body size at all then this would be a bad thing to do - instead we should have models that have the grouping variables without log.body included to assess the possibility that the different groupings of taxa are all we needed to understand differences in brain size, and that knowing the body size was not needed. Essentially, by structuring the analysis the way I did we took as a given that bigger animals should have bigger brains, and we focused only on which taxonomic grouping added the most to our understanding. The point is not that this was either a correct or incorrect choice, but just consider that your choices of models affects what you learn from the analysis.
8. Using model selection doesn't relieve us of the responsibility to make sure that our model fits the data. Ultimately it only really matters that the models we interpret meet GLM assumptions, so we will focus on dpo.lm and dpo.int.lm. In the chunk check.assumptions of your Rmd file enter:
par(oma = c(0,0,3,0), mfrow = c(2,2))
plot(models.list$dpo.lm)
plot(models.list$dpo.int.lm)
You'll see that the residual plots look really good - these models fit well.
We don't need to worry about whether poorly supported models meet GLM assumptions, because one of the reasons they might not is that they don't include the right predictors, and that is already accounted for when we compare AICc values. For example, if there are groupings in the data we're not accounting for in our categorical predictors, or differences in slopes of lines that we haven't accounted for with an interaction term, or some such failure of our model to properly represent the structure of the data, the models that fit poorly because of these issues will have high AICc values and won't be interpreted. But, for the models we do want to interpret we should confirm we are meeting the assumptions of our linear models so that we know that our interpretations will be accurate.
9. One last thing before we put too much confidence in our best-supported models are: we need to stop and remember that "best supported" is a relative term, and it is only meaningful relative to the models we've included in the analysis. With our analysis of brain sizes, all we have done so far is to establish that models that include the dpo predictor along with log.body are well supported compared to models that use other groupings of the taxa. But, it could be that dpo.lm and dpo.int.lm are just the best of ten terrible models.
For example, we could get big differences in AICc between models with multiple R2 of 0.1, 0.01, 0.001, or 0 (with 0 for the R2 of the intercept-only model), but the best of this sorry bunch still only explains 10% of the variation in the response and should not be the basis for any firm conclusions about what determines brain size. We do not have a large sample size here, but the point is even more important with larger data sets, because the amount of difference btween the AICc values gets bigger for a given effect size with larger sample sizes.
So, in addition to dAiCc and model weights, we should always have a measure of how well the model explains variation in the response variable. We can extract the multiple R2 for each of the models with (in the extract.r.squared chunk of the Rmd file):
sapply(models.list, FUN = function(x) summary(x)$r.squared)
You should see the following:
body.lm taxa.lm
taxa.int.lm
dino.lm dino.int.lm
0.5995125
0.9765490
0.9790453
0.9227799 0.9247020
primate.lm
primate.int.lm
dpo.lm dpo.int.lm intercept.only.lm
0.6924136
0.6925171
0.9644556
0.9705627 0.0000000
Aside from the intercept only model, which explains no variation in the response at all and will always have an R2 of 0, all of the other models have R2 of 0.6 or higher. The best-supported models have values of 0.96 or 0.97, which are close to perfect. From this we can conclude that the best supported models are also very good models of variation in brain size for these species.
What more do you want to know?
We won't be taking the interpretation of our models any further today for lack of time, but if we were, all of the interpretation steps we have used all semester are still appropriate here. For example, our models are ANCOVA's, so for the best supported models we could:
-
Use least squares means to compare the brain sizes across the levels of the dpo categorical variable, for dpo.lm
-
Compare the slopes across the categories for dpo.int.lm
That's it! Knit and upload your Word file and you're all done. Next stop, final exam!
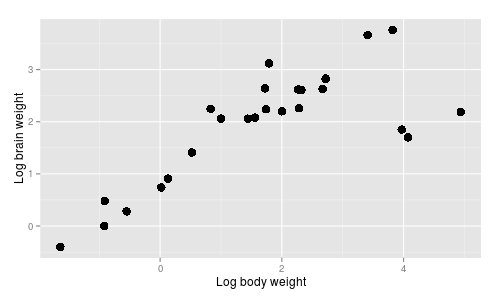 The brain/body data is shown in
the graph to the right. Brain and body weight have both been log-transformed, which makes the
relationship linear...which, by the way, tells you that brain and body weight have what kind of
relationship?
The brain/body data is shown in
the graph to the right. Brain and body weight have both been log-transformed, which makes the
relationship linear...which, by the way, tells you that brain and body weight have what kind of
relationship? 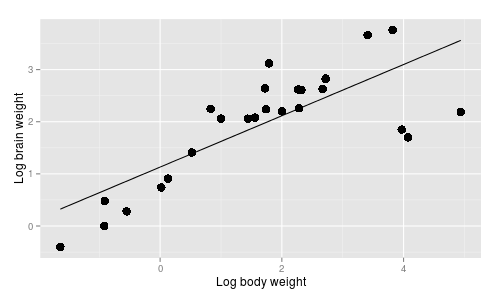 One possibility is that brain/body
scaling is the same for all species, regardless of the taxonomic group they belong to, and a simple
linear regression of log.brain on log.body would represent this hypothesis, like the graph to the right.
One possibility is that brain/body
scaling is the same for all species, regardless of the taxonomic group they belong to, and a simple
linear regression of log.brain on log.body would represent this hypothesis, like the graph to the right.