Recall from our statistics review that the ANOVA approach to analyzing differences between three or more groups is to:

We do this odd two-step procedure to avoid excessive false positive errors. Post-hoc procedures adjust the comparisons of group means so that a larger difference is needed to achieve statistical significance, so that across all of the tests conducted the family-wise error rate is kept at the chosen (nominal) α level of 0.05.

After we review a few of the available post-hoc procedures, we will learn to use orthogonal contrasts. Orthogonal means independent, and when comparisons are independent it is not necessary to adjust for multiple comparisons - these orthogonal contrasts therefore have higher statistical power than post-hoc procedures (that is, they have a greater chance of detecting a real effect, and thus have a greater sensitivity than post-hocs). One common type of orthogonal contrasts is the orthogonal polynomial, which can be used to analyze patterns of change in response across ordinal categories - we will learn to use orthogonal polynomials. You can also construct your own contrasts (either orthogonal or not) and test them - there is an optional section at the end of the assignment that shows you how.

Lastly, when comparisons are made for different variables made on the same experimental subjects the tests are not independent and can lead to excessive false positive errors. We will learn to use adjustments to the α level that account for this effect.

Post-hoc procedures

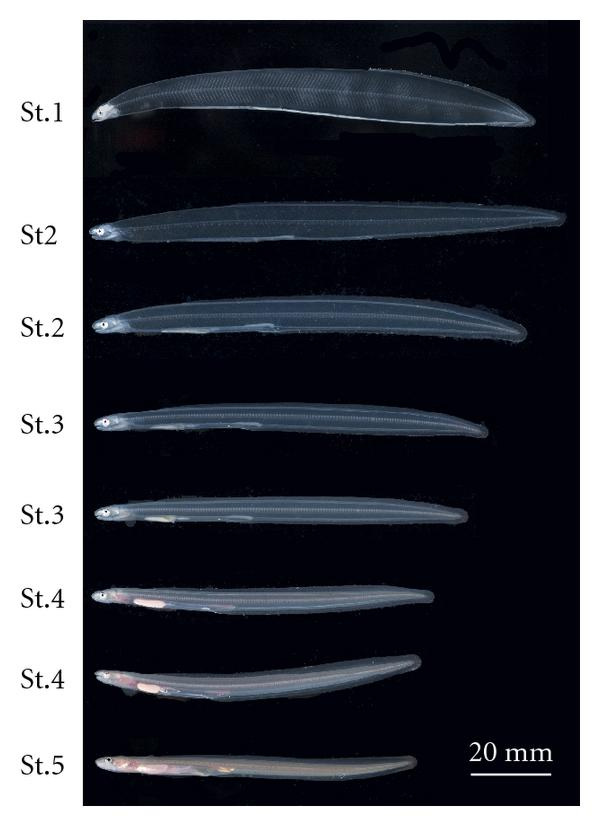Eel larvaeWe will be working with the conger eel data set presented in lecture - it is a study by Kawakami et al. 2009 of changes in water, neutral sugars, and hyaluronan during larval development. Illustrations of the five larval stages are shown to the left (two images are given for stages 2, 3, and 4). Because larval development is a process that occurs in sequence over time, developmental stage is an ordinal categorical variable.

Import, summarize, and graph the data

Start R Studio and make a new project for today's assignment. The eels.xlsx data set is here, and the posthocs.Rmd R markdown file to use today is here.

1. Import the eels.xlsx file into an R data set called "eels". Put the commands in chunk eels.import.data of your Rmd file.

By default columns of text are imported as character data. R has a special data type for variables that are meant to be used to define groups in a model, called a factor, and we can convert Stage to a factor before using it (in your Rmd file, just below your read_excel() command):

eels$Stage <- factor(eels$Stage)

This command takes the text labels in eels$Stage, converts them to a factor made up of levels (using factor(Stage)), and assigns the result back into eels$Stage, thereby replacing the non-factor version with the factor we just created. Note that we didn't bother to list the levels this time - alphabetical order is also increasing developmental stage order, so the factor() command's default works fine here.

2. You can now plot the means and 95% confidence intervals for hyaluronan (HA) by developmental stage (Stage). We are going to focus on HA for this exercise, since it has an interesting pattern of change across the stages of development. We have done this type of graph a few times now - use summarySE() from Rmisc to get the summary data to plot (summarize.data chunk of your Rmd file), and use ggplot2's ggplot() command to make your graph (plot.means.ci chunk of your Rmd file).

3. Fit a linear model of HA as a function of Stage, and call it eels.ha.lm - put the command in the fit.lm chunk of your R markdown file. Once you have it, also get the ANOVA table (enter the anova() command below the lm() command in the same chunk). You'll see that HA differs significantly between developmental stages.

Now that we have a fitted model, we can do some post-hoc procedures to address which of the groups are different from one another. Which we choose depends on which means we want to compare.

Tukey post-hocs - all possible pairs of means

You already know about Tukey tests - the Tukey procedure compares every possible pair of means, of which there are k(k-1)/2, or 5(4)/2 = 10 with our five stages of development. The amount of adjustment depends on the number of tests, and with 10 comparisons it will take a pretty big difference to be statistically significant - this will protect against Type I (false positive) errors, but at the expense of potentially missing smaller differences (Type II, false negative errors).

4. We can't use the TukeyHSD() command we learned in the review, because it doesn't work on lm() objects. The command we will use to get Tukey tests from our GLM is part of the "emmeans" package. If you're working on a computer on campus, or through Cougar Apps it is already installed and just needs to be loaded - you can load it using the command (in the load.emmeans chunk of your R markdown file):

library(emmeans)

If you are working on your own computer you can install the emmeans library first in the Packages tab, and then add the library(emmeans) to your code.

The emmeans package is...wonderful. I only recently started using it myself, and it is so good that I had to re-write this entire exercise to take advantage of its capabilities, which dramatically shortened and simplified the instructions (pity the students who came before you!). We will use it throughout the semester for multiple comparison procedures, graphs, and estimates of marginal means (or "least squares means" as they are sometimes called).

The emmeans library uses a single command, emmeans(), for all of its post-hocs, with arguments that indicate the kind of post-hoc to return. To get Tukey post-hocs, type the command (in the tukey.emmeans chunk of your R markdown file):

emmeans(eels.ha.lm, tukey ~ Stage) -> eels.ha.emm

eels.ha.emm

You will see all ten of the comparisons that can be made between the five stages, along with their p-values, reported:

$emmeans
 Stage   emmean   SE df lower.CL upper.CL
 Stage 1    564 36.4 15    486.3      641
 Stage 2    636 36.4 15    558.2      713
 Stage 3    406 36.4 15    328.2      483
 Stage 4    271 36.4 15    193.5      348
 Stage 5    104 36.4 15     26.1      181

Confidence level used: 0.95

$contrasts
 contrast          estimate   SE df t.ratio p.value
 Stage 1 - Stage 2    -71.9 51.4 15  -1.397  0.6384
 Stage 1 - Stage 3    158.1 51.4 15   3.075  0.0513
 Stage 1 - Stage 4    292.8 51.4 15   5.695  0.0004
 Stage 1 - Stage 5    460.2 51.4 15   8.950  <.0001
 Stage 2 - Stage 3    230.0 51.4 15   4.472  0.0035
 Stage 2 - Stage 4    364.7 51.4 15   7.092  <.0001
 Stage 2 - Stage 5    532.1 51.4 15  10.348  <.0001
 Stage 3 - Stage 4    134.7 51.4 15   2.620  0.1163
 Stage 3 - Stage 5    302.1 51.4 15   5.876  0.0003
 Stage 4 - Stage 5    167.4 51.4 15   3.256  0.0365

P value adjustment: tukey method for comparing a family of 5 estimates 

The output is in two blocks:

Tukey post-hocs use a sampling distribution that changes shape depending on the number of comparisons being done, so you can continue to interpret Tukey p-values below 0.05 to be significant without inflating your overall Type I error rate.

Quick aside about the table of emmeans - it seems to be giving you the same information as the table you made with summarySE() - that table is here for reference (I added the lower and upper limits of the 95% confidence interval for comparison):

    Stage N       HA       sd       se        ci     lower    upper
1 Stage 1 4 563.8025 92.11653 46.05827 146.57796 417.22454 710.3805
2 Stage 2 4 635.6600 92.03236 46.01618 146.44403 489.21597 782.1040
3 Stage 3 4 405.7000 54.96816 27.48408  87.46660 318.23340 493.1666
4 Stage 4 4 270.9675 24.77444 12.38722  39.42166 231.54584 310.3892
5 Stage 5 4 103.5575 76.49631 38.24815 121.72269 -18.16519 225.2802

But, if you look at the numbers you'll see that the means match, but the standard errors and CI's are not the same.

The reason they are different is that emmeans() generates its table from the fitted model. We assume that the data are normally distributed and have equal variances, and if this is the case our best estimate of the amount of random variation in the data comes from all the data combined - that is, it comes from the MSresidual term for the overall fitted model. Using all of the data also allows us to use a larger total sample size in calculating the standard errors, so the standard errors are all the same and generally smaller in the emmeans table than in the summarySE() table.

Which is correct? Depends on what you want to know:

5. A list of 10 comparisons is difficult to interpret. A simpler presentation that is easier to understand is the "compact letter display", which we can get with the command (put below the previous commands in the same code chunk, in your R markdown file) - note that this hasn't been working consistently for some reason, skip if it doesn't work for you:

multcomp::cld(eels.ha.emm)

This style of command gives the name of a package, followed by two colons, followed by the command within the package that you want to use. If you are working at home, you may need to install the multcomp library before you can use this command.

The cld() command gives you output that looks like this:

  Stage   emmean   SE df lower.CL upper.CL .group
 Stage 5    104 36.4 15     26.1      181  1   
 Stage 4    271 36.4 15    193.5      348   2  
 Stage 3    406 36.4 15    328.2      483   23 
 Stage 1    564 36.4 15    486.3      641    34
 Stage 2    636 36.4 15    558.2      713     4

Confidence level used: 0.95
P value adjustment: tukey method for comparing a family of 5 estimates
significance level used: alpha = 0.05
NOTE: Compact letter displays can be misleading
      because they show NON-findings rather than findings.
      Consider using 'pairs()', 'pwpp()', or 'pwpm()' instead.

The compact letter display assigns the same number in the .group column to stages that are not significantly different, and assigns different numbers to stages that are significantly different (why not letters? Only the programmers know). If more than one number is assigned to a stage that means that the stage isn't different from either of the stages it shares a number with - for example, Stage 1 is assigned 3 and 4 (not 34), so it isn't different from stages that have a 3 (Stage 3) or stages that have a 4 (Stage 2). From the output you can see that Stage 5 is different from all the others. Identify the rest of the differences that are significant and record them in your R markdown file.

The somewhat snarky note you get when you use the cld() command on an emmeans() results object indicates that statisticians do not always agree - the "NOTE" warning you to use a better method reflects the fact that the emmeans developers disagree with the multcomp developers about the utility of a compact letter display. Personally, I find them helpful in summarizing a long list of results in a more compact and understandable format.

Dunnett's post-hocs - comparison with the control group

Adjusting for 10 comparisons is extravagant if you only actually care about a few of them. For example, it is not uncommon to care primarily whether a set of treatment groups differ from the control, but not whether the treatments are different from one another. We don't have a control group per se, but if we are only interested in when the eels start to differ from their Stage 1 starting point we could use Dunnett's tests, which compare each mean to a single group - with five groups this means we will only have to correct for 4 comparisons if we use Dunnett's tests instead of 10, and smaller differences will be detectable.

6. You can get Dunnett's comparisons with emmeans by changing the tukey ~ Stage argument to dunnett ~ Stage. In the dunnett.emmeans chunk of your R markdown file enter:

emmeans(eels.ha.lm, dunnett ~ Stage)

You'll see that the output still reports means for every stage in the $emmeans section, but this time the comparisons in $contrasts are only between Stage 1 and each of the other four.

If you compare the p-values for the comparisons of each stage to Stage 1 that you get with Dunnett to the same comparison using Tukey tests, you'll see that Dunnett's gives you smaller p-values for the same comparison. Reducing the number of tests done makes it possible to detect smaller differences.

The Dunnett procedure in emmeans assumes the "control" group is the first level in the variable, Stage 1 in this case. To pick a different stage you would either need to make a factor with the levels in the order you want (whichever is first being the "control" for Dunnett's tests), or you can use the trt.vs.ctrlk option in emmeans - to use Stage 2 as the control you would use (in the console):

emmeans(eels.ha.lm, trt.vs.ctrlk ~ Stage, ref = 2)

You will still get Dunnett comparisons, but this time with every group compared to Stage 2 as the reference group.

Sequential comparisons - comparing each level to the previous one

Instead of comparing treatments to a control we might only be interested in whether each stage differs from the previous one - that is, we may want to know if there are changes from one stage to the next during development. We can get these comparisons using (in the consec.emmeans chunk of your Rmd file):

eels.ha.consec <- emmeans(eels.ha.lm, consec ~ Stage)

eels.ha.consec

You'll see that each level is compared to the one before it.

Ordinal categorical variables and orthogonal polynomials:

So far none of the methods we used made full use of the fact that Stage is an ordinal variable. The closest we came was in our selection of consec comparisons, which compared stages to those that came before them, but there was no consideration of the pattern of change across the levels. When we have numeric predictors we are primarily interested in the pattern of change - we fit a line to the data and interpret the slope of the line, rather than comparing group means. Here we have levels that do not have a quantitative relationship with one another, but they do have a natural order, and we can ask how HA changes across developmental stages using orthogonal polynomial contrasts.

Orthogonal polynomials are the default contrasts R uses for ordered factors, so all we need to do to get them is to make an ordered factor out of Stage.

1. We will make an ordered factor out of Stage, but will assign it to a new variable called Stage.ordered so that Stage can continue to function as an un-ordered factor. We'll then use Stage.ordered in our lm() to get orthogonal polynomial contrasts.

To make an ordered factor called "Stage.ordered", you can add "ordered = T" as an argument to the factor() command, like so (in the stage.ordered chunk of your R markdown file):

eels$Stage.ordered <- factor(eels$Stage, ordered = T)

Note that we can make an ordered factor just by adding ordered = T to the factor() command, rather than using the ordered() command.

If you type eels$Stage.ordered at the console you'll see the stage names with the factor levels listed at the bottom - the levels will be separated by less than symbols, <, indicating that R now knows that levels increase from left to right.

Before we run the analysis, let's take a look at what the orthogonal polynomial contrasts actually look like - in the console enter:

contr.poly(5)

This will show you the weights used to make orthogonal polynomial contrasts for 5 levels of a factor, like so:

             .L         .Q            .C         ^4
[1,] -0.6324555  0.5345225 -3.162278e-01  0.1195229
[2,] -0.3162278 -0.2672612  6.324555e-01 -0.4780914
[3,]  0.0000000 -0.5345225 -4.095972e-16  0.7171372
[4,]  0.3162278 -0.2672612 -6.324555e-01 -0.4780914
[5,]  0.6324555  0.5345225  3.162278e-01  0.1195229

Instead of comparisons between specific group means, these weights define the pattern of change expected for a factor with five levels. The patterns are read down the columns, and the labels indicate the linear trend (.L), quadratic trend (.Q), cubic trend (.C), and fourth (^4) order trends. The patterns are:

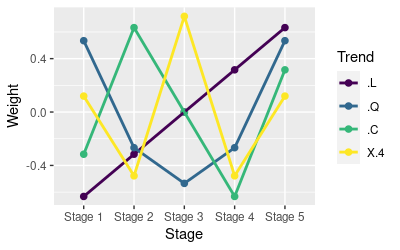
A graph of the weights is shown to the left. The exact values of the weights aren't important, but there are a couple of rules for selecting them:

You can confirm the sum of products criterion with a quick calculation - first, you can multiply the linear column by each of the others with (in the console):

contr.poly(5) -> poly.wts

poly.wts[,1] * poly.wts[,-1]

This command multiplies the .L column from poly.wts (.L is column 1) by every column except the .L column (column -1 omits .L). To confirm that these sum to 0 use (in the console):

colSums(poly.wts[,1] * poly.wts[,-1])

You should get numbers such as -1.110223e-16. This is a number in R's scientific notation format, and it means -1.110223 x 10-16, which is a very small number, very close to 0 (it is only not exactly zero because of rounding error). You can do the same calculation for any of the columns 2 through 4 and you should see the same thing, confirming that this set of weights produces independent contrasts.

You can confirm that each set of weights sums to zero with (in the console):

colSums(poly.wts)

You'll see tiny numbers very close to 0.

These are used just like the dummy coded columns we made last week - each row is the set of weights for each stage. Combined with the data set they look like this:

     Stage     HA         .L         .Q            .C        X.4
1  Stage 1 446.86 -0.6324555  0.5345225 -3.162278e-01  0.1195229
2  Stage 1 654.96 -0.6324555  0.5345225 -3.162278e-01  0.1195229
3  Stage 1 537.08 -0.6324555  0.5345225 -3.162278e-01  0.1195229
4  Stage 1 616.31 -0.6324555  0.5345225 -3.162278e-01  0.1195229
5  Stage 2 647.47 -0.3162278 -0.2672612  6.324555e-01 -0.4780914
6  Stage 2 593.92 -0.3162278 -0.2672612  6.324555e-01 -0.4780914
7  Stage 2 758.05 -0.3162278 -0.2672612  6.324555e-01 -0.4780914
8  Stage 2 543.20 -0.3162278 -0.2672612  6.324555e-01 -0.4780914
9  Stage 3 446.74  0.0000000 -0.5345225 -4.095972e-16  0.7171372
10 Stage 3 431.83  0.0000000 -0.5345225 -4.095972e-16  0.7171372
11 Stage 3 419.24  0.0000000 -0.5345225 -4.095972e-16  0.7171372
12 Stage 3 324.99  0.0000000 -0.5345225 -4.095972e-16  0.7171372
13 Stage 4 297.87  0.3162278 -0.2672612 -6.324555e-01 -0.4780914
14 Stage 4 286.06  0.3162278 -0.2672612 -6.324555e-01 -0.4780914
15 Stage 4 251.97  0.3162278 -0.2672612 -6.324555e-01 -0.4780914
16 Stage 4 247.97  0.3162278 -0.2672612 -6.324555e-01 -0.4780914
17 Stage 5 201.34  0.6324555  0.5345225  3.162278e-01  0.1195229
18 Stage 5 125.65  0.6324555  0.5345225  3.162278e-01  0.1195229
19 Stage 5  30.96  0.6324555  0.5345225  3.162278e-01  0.1195229
20 Stage 5  56.28  0.6324555  0.5345225  3.162278e-01  0.1195229

You'll see each of the numbers in the first row of the weights matrix are used for each Stage 1 row of the data set, each of the numbers in the second row of the weights matrix are used for Stage 2, and so on. Just like dummy codes, these polynomial weights are then used in a multiple regression to test for a linear, quadratic, cubic, or fourth degree pattern.

Now we just need to use Stage.ordered in an lm() to test for these four patterns of trend in the HA data.

2. Run a GLM model with an ordered factor as a predictor (in the lm.with.polynomial.contrasts chunk of your R markdown file):

eels.op.lm <- lm(HA ~ Stage.ordered, data=eels)

This command fits exactly the same linear model as we used before, with HA predicted by Stage, but by using Stage.ordered we prompt R to use polynomial contrasts instead of dummy codes to represent the group means. Get the ANOVA table for this model (anova.poly.weights chunk of your R markdown file):

anova(eels.op.lm)

and you will get an ANOVA table that matches the one you got with Stage as an unordered factor. Using orthogonal polynomial weights doesn't change the ANOVA table.

Just like with dummy codes, four columns can represent five group means perfectly, so even though we used polynomial weights we can still get Tukey tests from this model if we want to. Confirm that Tukey tests from this model are the same as for the unordered version of Stage (in the tukey.poly.weights chunk of your R markdown file):

emmeans(eels.op.lm, tukey ~ Stage.ordered)

The comparisons of means is exactly the same as before - using polynomial weights doesn't prevent you from comparing group means if that's what you want to do.

Where the results do differ between ordered and unordered factors is in the coefficients, which you can see with the command (in the coefficient tests.poly.weights chunk of your R markdown file):

summary(eels.op.lm)

The model output looks like this:

Call:
lm(formula = HA ~ Stage.ordered, data = eels)

Residuals:
    Min      1Q  Median      3Q     Max
-116.94  -43.12   12.68   30.44  122.39

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)       395.94      16.26  24.349 1.79e-13 ***
Stage.ordered.L  -406.41      36.36 -11.177 1.13e-08 ***
Stage.ordered.Q  -102.44      36.36  -2.817   0.0130 *  
Stage.ordered.C    85.11      36.36   2.341   0.0335 *  
Stage.ordered^4   -62.74      36.36  -1.726   0.1050    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 72.72 on 15 degrees of freedom
Multiple R-squared:  0.904,    Adjusted R-squared:  0.8785
F-statistic: 35.33 on 4 and 15 DF,  p-value: 1.805e-07

If you compare the model summary output here to what you got with the unordered version of stage, the bottom-most section is identical - using an ordered factor doesn't change the fit, degrees of freedom, or overall p-value for the model. But, the coefficient tests are now tests of trend across the ordered stage levels. You'll see that the linear (.L), quadratic (.Q), and cubic (.C) terms are significant, but the fourth degree (^4) term is not.

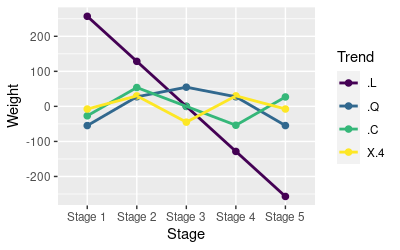
The graph on the left shows how the coefficients modify the weights to fit to the HA data. The sign on the coefficient keeps the pattern the same if it is positive, but it flips the pattern around the x-axis if it is negative. The magnitude of the coefficient indicates how strong the pattern is. So, for example, the linear trend (.L) has a negative sign, which flips the trend from positive to negative, and it has the largest magnitude, so it is the strongest pattern in the data - the straight line covers the widest range of values along the y-axis in this graph.

When you interpret orthogonal polynomials, remember that they add together. So...

These orthogonal polynomial trend results match our impression from looking at the graph nicely, and provide us with some statistical support for claiming that HA peaks at the second stage and declines for the remaining stages. They do not test for differences between any pair of means, but if the question you are interested in is about the pattern of change across ordinal categories, orthogonal polynomials are very useful.

Many ways there are

R uses orthogonal polynomial contrasts by default when you use an ordered factor as a predictor. But, it isn't necessary to make a factor ordered to get orthogonal polynomial contrasts - provided that the order of the levels is in the sort order you want, you can instead either specify the contrasts in your lm(), or you can set the type of contrasts by assigning them to the variable in your data frame.

To specify them in the lm() we would use:

lm(HA ~ Stage, data = eels, contrasts = list(Stage = "contr.poly"))

This approach doesn't change the Stage variable, but produces the same result as making Stage an ordered factor.

Or, rather than making Stage.ordered we could have just assigned the contrasts we wanted to use to the Stage variable, like so:

contrasts(eels$Stage) <- contr.poly(5)

Then using lm(HA ~ Stage, data = eels) would give us orthogonal polynomial contrasts without having to specify them in the lm(). To set the contrasts back to the default dummy coding we would use:

contrasts(eels$Stage) <- contr.treatment

R calls dummy coding "treatment contrasts", so this command assigns the default treatment contrasts to Stage.

Note that we could have also gotten orthogonal polynomial contrasts from emmeans() after we had already gotten a fitted model that used dummy coded predictors - if we used:

emmeans(eels.ha.lm, poly ~ Stage)

we get:

$contrasts
 contrast  estimate  SE df t.ratio p.value
 linear       -1285 115 15 -11.177  <.0001
 quadratic     -383 136 15  -2.817  0.0130
 cubic          269 115 15   2.341  0.0335
 quartic       -525 304 15  -1.726  0.1050

The t-values and p-values are the same, but the estimates are not - this is almost certainly due to a difference in how emmeans() assigns weights, but I haven't figured out what the difference is yet. Either approach is fine, though, since the p-values match, and the magnitudes of the estimates matter less than their signs and sizes relative to one another.

Long story short - R is flexible, and there are usually multiple ways to accomplish the same thing. This can be confusing to beginners, but it can be an advantage as you move into more advanced applications.

Corrections for multiple comparisons outside of an ANOVA

The contrasts and post-hoc procedures we've learned all apply to a single factor in an ANOVA. But, it is not uncommon to have more than one response variable measured in a single experiment, and we would want to analyze all of them. The data set we have for the eel study has three different response variables, all measured from the same eels, and they are not independent - the correlation between HA and NS is r = -0.77, between HA and water is r = 0.75, and between NS and water has r = -0.56 (if they were independent the correlation would be 0). Since the variables are not independent it seems we should make some sort of correction for multiple comparisons, but if we are fitting three separate models it's not straightforward to incorporate this correction into our post-hoc procedures.

When we are in this situation, we can account for the additional chances of Type I errors by adjusting the alpha level for our analyses. The simplest correction for the alpha level commonly used is the Bonferroni. Bonferroni's correction sets a nominal alpha level, or family-wise error rate, at a desired level (usually the traditional 0.05) and then calculates the alpha level used for each test by dividing the nominal level by the number of tests conducted. If we were to test for differences among stages in water as well as HA we would be producing two omnibus tests, with two p-values, and could test each at 0.05/2 = 0.025 to avoid an increase in Type I error rate. If we also tested NS, we could test at 0.05/3 = 0.0167.

However, Bonferroni's correction is stronger than absolutely necessary. If we assume that each test has a 5% chance of a false positive, then it also has a 95% chance of a correct negative. Across three comparisons the chance of correct negatives on all of them is 0.95 x 0.95 x 0.95, or (1 - 0.05)3. Any other possible outcome other than this would include a false positive, Type I error in at least one comparison, so the probability of one or more false positives across these five comparisons is 1 - (1 - 0.05)3. If we wanted to achieve an overall family-wise rate of 0.05, we could set this quantity equal to 0.05, and then solve for the level that we would need to test at to achieve a family-wise rate of the desired 0.05 value. In other words:

0.05 = 1 - (1 - α)3

α = 1-(1-0.05)1/3 = 0.0169

This is called the Dunn-Sidak correction, and you can see it is a little bit bigger than Bonferroni, and thus a little more easier to achieve statistical significance with, without increasing the false positive rate.

Let's see how correcting for multiple p-values affects our interpretation of the data. Do the following steps in your R markdown file.

1. Fit a model using water as a response, and Stage as a predictor, and then get an ANOVA table to test for an effect of Stage (chunk water.lm).

2. Fit a model using NS as a response, and Stage as a predictor, and then get an ANOVA table to test for an effect of Stage (chunk ns.lm).

3. Calculate the two corrections we could use - enter (adjusted.alphas):

0.05/3

1 - (1-0.05)^(1/3)

The first calculation is the Bonferroni correction, and the second is Dunn-Sidak. These two values are the corrected alpha-levels we should use to assess if the p-values are statistically significant from our three linear models. Compare the p-values from each of the models and see if any of them are no longer significant after adjustment. The variable that was significant at 0.05 but not at these adjusted levels could be a Type I error if we were to use the 0.05 level.

In summary...

To wrap up this collection of procedures:

Optional: custom post-hocs and contrasts

There are several additional built-in comparisons in emmeans that we didn't go over (you can read about them if you type "contrast-methods" in the search bar in R Studio's Help tab). But, if you want to make a set of comparisons that are not already available, you can specify your own.

We'll try out a couple of custom contrasts to see how they work.

1. First we need to make a set of vectors that define each group by placing a 1 in the position occupied by the group. For example, the mean of Stage 1 is identified with (in the group.vectors code chunk of your R markdown document):

s1 <- c(1,0,0,0,0)

This set of weights has a 1 in the first position to represent Stage 1, and a zero for the other four positions for the rest of the stages.

To make the remaining comparisons, you need a vector for each one (add to your R markdown document, same code chunk, below s1):

s2 <- c(0,1,0,0,0)

s3 <- c(0,0,1,0,0)

s4 <- c(0,0,0,1,0)

s5 <- c(0,0,0,0,1)

2. To define the contrasts, we need to decide what comparisons we want to make, and then make them on these group vectors - the result will then be used as the weights when we do our contrasts. For example, if we wanted to compare the average of groups 1 and 2 to the average of groups 4 and 5, we would do the following (in the console):

(s1+s2)/2 - (s4+s5)/2

You'll see that the output you get is another vector that looks like this:

0.5  0.5  0.0 -0.5 -0.5

When you use vectors in mathematical expressions R operates on the matching elements, so adding s1 to s2 produced a vector with elements 1,1,0,0,0, and dividing by 2 resulted in 0.5, 0.5, 0, 0, 0. The same is true for the (s4+s5)/2 operation, which produced a vector with 0,0,0,0.5,0.5. Subtracting the (s4+s5)/2 vector from the (s1+s2)/2 vector gave us the final 0.5, 0.5, 0, -0.5, -0.5 vector in our output. These weights will result in a comparison of the mean of stages 1 and 2 to the mean of groups 3 and 4 - multiplying by half and then summing is equivalent to calculating the average of two groups, and the mean of the groups with negative weights will be subtracted from the mean of the groups with positive weights.

We could also decide we want to compare the mean of Stage 1 to the average of the rest of the stages, like so:

s1 - (s2 + s3 + s4 + s5)/4

which gives us:

1.00 -0.25 -0.25 -0.25 -0.25

This set of weights will compare the Stage 1 mean against the mean of the other four stages. Note that the two contrasts have weights that sum to zero, but the sums of the products of the weights for the two contrasts is not equal to 0, so they are not independent - we will need to correct for multiple comparisons when we run them.

To get emmeans() to use these contrasts, and correct for the fact that we are doing two comparisons, we need to put them both into an R list (in the define.contrasts chunk of your Rmd file):

list(s1s2.vs.s4s5 = (s1+s2)/2 - (s4+s5)/2, s1.vs.s2s3s4s5 = s1 - (s2+s3+s4+s5)/4) -> custom.contrasts

Note that when we define the list we name each element in a way that identifies which means are being compared, and then create the element by putting the calculations we did above into the function definition of the element. For example, the first named element is s1s2.vs.s4s5, and we assign it the mean of s1 and s2 minus the mean of s4 and s5. Naming the elements of the list isn't necessary, but it makes the results easier to interpret since these names will be used to label the final output. To see what this list contains, type custom.contrasts in the console:

$s1s2.vs.s4s5
[1]  0.5  0.5  0.0 -0.5 -0.5

$s1.vs.s2s3s4s5
[1]  1.00 -0.25 -0.25 -0.25 -0.25

2. To use these to get multiple comparisons, we first use emmeans() to make an object with all the needed values (means, standard errors, sample sizes), and then we use the contrast() function on the emmeans() object to test the contrasts for statistical significance (in your Rmd file, test.custom.contrasts chunk):

emmeans(eels.ha.lm, ~Stage) -> eels.ha.emm

contrast(eels.ha.emm, custom.contrasts, adjust = "mvt")

The output of this command is:

  contrast       estimate   SE df t.ratio p.value
 s1s2.vs.s4s5        412 36.4 15  11.344  <.0001
 s1.vs.s2s3s4s5      210 40.7 15   5.162  0.0002

P value adjustment: mvt method for 2 tests 

The first emmeans() command generates the estimated means and their standard errors, and then the contrast() function compares the means based on the contrasts we put in the custom.contrasts list object. We also tell contrast() to adjust for multiple comparisons using the "mvt", or multivariate, method, which is the default used by emmeans for custom contrasts. Since the contrasts are being corrected for multiple comparisons you can interpret p-values less than 0.05 as being statistically significant without risking an inflated false positive error rate.

Planned comparisons: orthogonal contrasts

It's possible to make comparisons between group means without having to adjust for multiple comparisons, if the comparisons are independent. We did this when we used orthogonal polynomials above, but it's possible to construct contrasts that are comparisons of group means that are also orthogonal.

There are at most k - 1 independent contrasts possible, where k is the number of groups - for the Stage variable there are at most 5-1 = 4 orthogonal contrasts. Orthogonal contrasts divide up the variation explained by the predictor variable into independent pieces, and then test those pieces for statistical significance. As was true for the orthogonal polynomial contrasts we used above, to be orthogonal the weights we use have to sum to 0 for any single contrast, and the sum of products of any two contrasts' weights has to be zero. This means that not every set of four contrasts that we could construct is independent - the Dunnett comparisons we used above were not, as you can see below.

Dunnett's comparisons

Factor levels Contrast 1 Contrast 2 Contrast 3 Contrast 4
Stage 1 1 1 1 1
Stage 2 -1 0 0 0
Stage 3 0 -1 0 0
Stage 4 0 0 -1 0
Stage 5 0 0 0 -1
Interpretation 1 vs. 2 1 vs. 3 1 vs. 4 1 vs. 5

The sums of the weights in each column are 0, but multiplying any two sets of weight together and summing the products gives a sum of 1, not 0 - which means that these comparisons are not independent. We were right to adjust the p-value for Dunnett's comparisons given this. You can confirm for yourself that sequential comparisons suffer from the same problem in the table below - if you enter a 1 and -1 for each pair of means being compared you'll see the sums of products aren't equal to 0.

Factor levels Contrast 1 Contrast 2 Contrast 3 Contrast 4
Stage 1
Stage 2
Stage 3
Stage 4
Stage 5
Column totals: 0 0 0 0
Contrasts: Sum of products
C1 vs. C2 0
C1 vs. C3 0
C1 vs. C4 0
C2 vs. C3 0
C2 vs. C4 0
C3 vs. C4 0

So, not every set of four contrasts will be independent, only ones with weights that meet our criteria are independent.

Each of the four sets of contrasts below do meet the criteria for being orthogonal - each column sums to 0, and the sum of the products of any two columns also sums to zero. Remember that when fractions are used an average of two or more group means is being calculated, and weights with different signs are being compared to one another, while weights with the same sign are being averaged together.

Set 1:

Factor levels Contrast 1 Contrast 2 Contrast 3 Contrast 4
Stage 1 1/2 1 0 0
Stage 2 1/2 -1 0 0
Stage 3 -1/3 0 1 0
Stage 4 -1/3 0 -1/2 1
Stage 5 -1/3 0 -1/2 -1
Interpretation Mean of 1, 2 vs. mean of 3, 4, 5 1 vs. 2 3 vs. mean of 4,5 4 vs. 5

Set 2:

Factor levels: Contrast 1 Contrast 2 Contrast 3 Contrast 4
Stage 1 1 0 0 0
Stage 2 -1/4 1 0 0
Stage 3 -1/4 -1/3 1 0
Stage 4 -1/4 -1/3 -1/2 1
Stage 5 -1/4 -1/3 -1/2 -1
Interpretation 1 vs. mean of 2-5 2 vs. mean of 3-5 3 vs. mean of 4-5 4 vs. 5

Set 3:

Factor levels: Contrast 1 Contrast 2 Contrast 3 Contrast 4
Stage 1 1 0 0 0
Stage 2 -1/4 1/2 1 0
Stage 3 -1/4 1/2 -1 0
Stage 4 -1/4 -1/2 0 1
Stage 5 -1/4 -1/2 0 -1
Interpretation 1 vs. mean of 2-5 Mean of 2,3 vs. mean of 4,5 2 vs. 3 4 vs. 5

Set 4:

Factor levels: Contrast 1 Contrast 2 Contrast 3 Contrast 4
Stage 1 1 0 0 0
Stage 2 -1/4 1/2 1/2 -1/2
Stage 3 -1/4 1/2 -1/2 1/2
Stage 4 -1/4 -1/2 1/2 1/2
Stage 5 -1/4 -1/2 -1/2 -1/2
Interpretation 1 vs. mean of 2-5 Mean of 2,3 vs. mean of 4,5 Mean of 2,4 vs. mean of 3,5 Mean of 3,4 vs. mean of 2,5

As an exercise, we'll use Set 4.

Since these are a little more complicated than the previous step, we'll make the vectors of weights first, assign each to an object, and then make our list of contrasts from these objects. First the vectors of weights (in the orthogonal.contrasts chunk of your Rmd file):

Contrast.1 <- s1 - (s2+s3+s4+s5)/4
Contrast.2 <- (s2+s3)/2 - (s4+s5)/2
Contrast.3 <- (s2+s4)/2 - (s3+s5)/2
Contrast.4 <- (s3+s4)/2 - (s2+s5)/2

Then put these into a list (make.contrast.list chunk of your Rmd file):

list(s1.vs.s2s3s4s5 = Contrast.1, s2s3.vs.s4s5 = Contrast.2, s2s4.vs.s3s5 = Contrast.3, s3s4.vs.s2s5 = Contrast.4) -> orthog.contrasts

You can now use contrast() to test these - since they are orthogonal no correction for multiple comparisons is needed (in your test.orthog.contrasts chunk of your Rmd file):

contrast(eels.ha.emm, orthog.contrasts)

Note that we're using the same eels.ha.emm object as we used for the custom contrasts above, the only difference is the list of contrasts used. The results are:

 contrast       estimate   SE df t.ratio p.value
 s1.vs.s2s3s4s5    209.8 40.7 15   5.162  0.0001
 s2s3.vs.s4s5      333.4 36.4 15   9.170  <.0001
 s2s4.vs.s3s5      198.7 36.4 15   5.464  0.0001
 s3s4.vs.s2s5      -31.3 36.4 15  -0.860  0.4033

All of the contrasts are significant except the last one comparing s3 and s4 to s2 and s5.

Orthogonal contrasts are great, but orthogonality requirements limit the questions you can address with them. But, if the questions you want to address can be expressed as orthogonal contrasts you will get better statistical power from them than from any post hoc procedure.

Assignment

All done! Save, knit, and upload your Word file with all your output.