Finding population growth rate from a life table
Now that we've confirmed that Solver can find solutions with its numerical approach that match analytical solutions we will switch to an example that has no analytical solution. As you learned in lecture, we can calculate a population growth rate from a life table using the Euler equation, which is Σlxbxe-rx. The value we want to calculate is r, and it isn't possible to solve for r. We will use Solver to estimate r numerically.
On the sheet "Life table", you have data on Chinook salmon survival and reproduction. The first column, "Stage", gives a name to each row of the table - the first row represents eggs laid, and the second row represents juvenile salmon that migrate to sea. The rest of the rows are the numbers of individuals that are adults for one year, two years, three years, and so on. The age (in years) that corresponds with each stage is in column B, and the number of individuals of each age is in C, labeled n(x). The numbers are standardized to start at 100,000 eggs laid, and you can see that for 100,000 eggs only 4800 juveniles will survive, only 336 will make it to their first year of adulthood, and only 57 live to be ten years old. The next column (D, labeled b(x)) is births per spawning adults.
To calculate population growth rate, we will need a column for survivorship (lx), the product of survivorship and birth rate (lxbx), and then the Euler equation calculation for each row (lxbxe-rx). We will use a cell in the spreadsheet (G13) to specify the growth rate (r) in the Euler equation. We will then sum the Euler column. With this setup, any time we change the value of r in cell G13 we will change the sum of the Euler values. By telling Solver to change the growth rate in G13 until the Euler sum in G15 is equal to 1, we can estimate the growth rate.
Step 1. Calculate lx
lx is the proportion of the total number originally in the population that is still alive at age x. In cell e2 type:
=c2/c$2
Copy and paste this to the rest of the cells in column E. Using an absolute reference to the second row for the denominator means that every value in the n(x) column is divided by the original number of salmon in value C2.
Step 2. Calculate lxbx
This is just the product of the lx and the bx column. For each cell, multiply the lx by the bx value in the same row. You can do this, make it so!
Step 3. Calculate the Euler value
Enter a starting value for r of 0 into cell G13.
Translate the Euler formula, (lxbxe-rx), into an Excel spreadsheet formula in cell G2, then copy and paste to the rest of the cells. Use G$13 as the value of r, and use the ages in column B for the value of x inside of your exp() function. Don't forget the minus sign on -rx.
Then, sum the values in G2 through G11 in cell G15.
If all went well, the sheet should look like this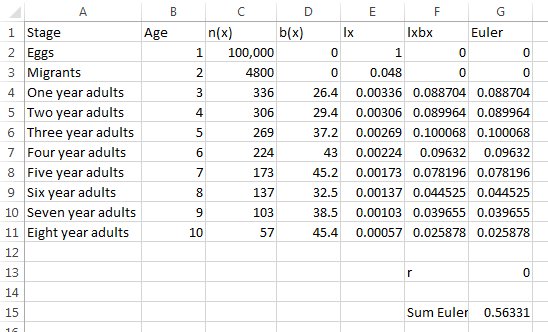 .
.
Step 4. Use Solver to find r.
Now, use Solver to find the growth rate for this population. To do this:
- Start Solver
- Use G15 as the objective
- Have Solver set the objective to 1
- Change the growth rate in G13
- Growth rates can be negative, so un-check the box that says "Make Unconstrained Variables Non-Negative" - also, make sure there are no constraints set (if there are any left from the previous Solver runs remove them)
Let Solver find a solution. You should see that it's a negative value (-0.09695), which is probably correct - most species of Pacific salmon are declining.
Step 5. Check for other possible solutions.
We can use our array formula skills for this step. We want to confirm that there is only one value of r that results in an Euler sum of 1, so let's start by making a range of r values in column i:
- Enter "r" in i1
- Enter the value -1 in i2
- Enter the value -0.9 in i3
- Select i2 and i3 and use the fill handle to extend the series to cell i22 - the value in i22 should be 1
Next enter the formula to calculate the Euler sum for r of -1:
- Enter "Sum Euler" in J1
- Enter the formula =sum(d$2:d$11*e$2:e$11*exp(-i2*b$2:b$11)) in cell J2 and use CTRL+SHIFT+ENTER to record it as an array formula - this does the same calculation we did in cell G15, but this time using the growth rate in i2
- Copy the cell and paste it to the rest of the cells below, J3 through J22
You'll see that the sum gets close to 1 at a growth rate of -0.1, which is close to the estimate in G13 of -0.09695. Below -0.1 the sums become huge, and above -0.1 they approach zero, so there is no reason to expect there to be more than one value that sets the Euler sum to 1 - our estimate of -0.09695 is the only solution we need to find.
Improving birth rate to stabilize the population
We can use numerical analysis to answer hypothetical questions as well - for example, this population is evidently in deep trouble, and if we wanted to do something about it we would need to improve survival or reproductive success, or both. We can use Solver to help us determine how much of an improvement in these demographic rates we would need to stabilize the population.
We'll start with improvements needed to reproduction.
Step 1: make a copy of the worksheet
We don't want to alter the actual table, so let's make a copy we can mess around with.
- Right-click on the "Life table" tab, and select "Move or copy"
- Check the "Create a copy" box, and select [move to end]
- Click "OK"
- Double-click on the new tab and change the name to "Reproduction"
Step 2: Move the b(x) column
We'll move the b(x) column down to the cells below it so that we can use them as the basis for altering the values in the table.
- Select cells D2 through D11
- Copy
- Paste to cell D14 (select D14 and paste - the entire set of b(x) values will be pasted in D14 through D23)
- Enter the label "Original b(x)" in cell D13
Step 3: Enter a multiplier that represents the amount of improvement needed
In cell D25 enter the value 1, and in C25 enter the label "Improvement needed"
Step 4: make the b(x) values equal to the original b(x) values multiplied by the improvement needed
In cell D2 enter a formula that multiplies D14 by D25 - use an absolute reference for the row in D25, and copy/paste the formula to the rest of the b(x) cells in D3 through D11.
To confirm this all worked, you should initially see the same b(x) values as before, because you're multiplying them all by 1. Set the improvement needed to 2 and you should get all the b(x) values in the table doubled.
Set the improvement needed back to 1 for the next step.
Step 5: use Solver to find the amount of improvement needed to stabilize the population
Now we're going to find the amount of improvement in birth rates needed to stabilize the population. A stable population has a growth rate of 0, so enter 0 into cell G13.
Start Solver, and this time:
- Use the sum Euler cell (G15) as the objective again, and have Solver set it to 1
- Change the Improvement needed in cell D25
You'll see that the improvement needed is 1.775221 - this means that we need to increase reproduction by 77.5% to stabilize the population.
Improving survival to stabilize the population
Make another copy of the Life table sheet, move it to the end of the workbook, and re-name it "Survival".
Copy and paste the as values the lx values in cells E2 through E11 - paste their values into cells C14 through C23, and label them in C13 "Original lx"
Enter the improvement needed in C25, and label it as "Improvement needed" in cell B25.
Start with the lx for the migrants - in cell E3 multiply the lx for migrants in cell c15 by the improvement needed in cell c25 (use an absolute cell reference for the rows of c25). Why not start with the eggs? Because the life table sets lx to 1 for eggs, and we can't do better than 100% survival.
Set growth rate to 0, and then use Solver to find the improvement needed to get the Euler sum back to 1.
You'll see that it would also take a 77.5% improvement in survival to stabilize the population.
Assignment
Done! Upload your completed spreadsheet with part 1 and part 2 to the course web site.