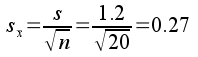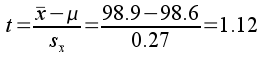Introduction

Bernie saves Pluto

You may have heard the myth that the Swiss would tie barrels of brandy to the necks of St. Bernard rescue dogs to warm up cold skiers in the Alps (this gif is from a Disney cartoon that depicts a St. Bernard giving a very cold Pluto a shot from his barrel. Binge drinking is not usually depicted in children's cartoons anymore - it was 1936, times have changed). The basis of this myth is the belief that drinking alcohol increases body temperature because people experience the sensation of warmth after drinking it. But, this subjective feeling of warmth may or may not reflect an actual increase in core body temperature.

How would we know if drinking brandy actually changes body temperature? As data-driven scientists, we should try to answer this question by devising an experiment to test whether drinking brandy changes core body temperature (and, no, this is not what we'll be doing in class this week, sorry to disappoint you).

As you know from our work on experimental design, to test the effect of brandy on body temperature we need to apply a treatment (brandy drinking) and measure a response (body temperature). One possible experiment that would test the hypothesis that drinking brandy affects core body temperature would be:

Brandy experiment: results

x̄ = 98.7°

s = 0.3

n = 20

If we conducted the experiment and got the results in the box on the right, the decision rules tell us that since the sample mean body temperature of x̄ = 98.7° is above 98.6° we should conclude that brandy increases body temperature.

That's what the data says, and you can't argue with the data. Right?

Random sampling strikes again

Unfortunately, it isn't so simple.

The problem is, the decision rules are not accounting for random sampling. According to the decision rules we can only conclude that drinking brandy doesn't affect core temperature if the mean for our data is exactly equal to 98.6°, and any differences, no matter how small, would cause us to conclude that brandy either increases or decreases body temperature.

This is a problem because the random samples we work with will produce some random variation in sample means. So, even if the population mean, μ, is exactly equal to 98.6°, the mean of a sample selected from that population, x̄, probably won't be. These differences would cause us to conclude that there is an effect of brandy on body temperature when there is not if we used decision rules that didn't account for random sampling.

The simulation to the right illustrates the problem - the data points represent a sample of 20 body temperatures selected from a population with a body temperature of μ = 98.6°, and the mean of the sample is reported below the graph. If you click the "Select a random sample" button a new sample of 20 is selected from the same population, which gives you a new sample mean. As you click repeatedly, note that the sample mean is rarely equal to 98.6°. Because of this random sampling variation, if we conclude that any mean other than exactly 98.6° indicates that brandy has an effect on body temperature then we will mistakenly conclude that brandy has an effect most of the time.

If you keep hitting "Select a random sample" you'll see that even though the mean is changing randomly, it isn't completely unpredictable. Means exactly equal to 98.6° don't happen very often, but means only rarely go as low as 98.5° or higher than 98.7°. This suggests a solution to our problem - even though a mean that is exactly equal to 98.6° isn't likely, we can change our decision rules to reflect the fact that small differences can happen by chance. If we can characterize the range of variation in sample means that random sampling usually produces then we can treat any observed difference that's within this range as probably being due to random chance, but treat sample means that fall outside of this usual range as probably being due to an actual effect of brandy on body temperature.

The question is, then, how different from 98.6° would our sample mean have to be to conclude that brandy has an actual effect on core temperature?

To answer that question we need inferential statistics, which are methods that allow us to draw conclusions about a population based on a sample of data. This week we will learn how to do a type of null hypothesis significance test (NHST), called a one-sample t-test, to determine if our sample mean of x̄ = 98.7° is different enough from 98.6° to conclude that drinking brandy increases body temperature.

Inferences are based on hypotheses

Before we learn about the one-sample t-test we will use in particular, we need to spend a little time on NHST's in general.

In the sciences, we base our conclusions on tests of hypotheses. In the sciences, a hypothesis is simply a possible explanation for some phenomenon. In inferential statistics we will call these sorts of statements of the way we think a system is working scientific hypotheses, although sometimes we will simply refer to the scientific hypothesis as the question we are trying to answer. For the current example, the scientific hypothesis is that brandy increases body temperature. The experiment we designed to test this question has us measuring body temperature, and we came up with some decision rules that tell us how to interpret the three possible outcomes of our experiment (i.e. an increase in temperature, no change, or a decrease in temperature). We use the scientific hypotheses to guide us in developing statistical hypotheses, and we revisit the scientific hypothesis after our statistical analysis is complete to draw a conclusion about whether the experiment supports our scientific hypothesis. This final decision will be based on our decision rules, modified to account for the effects of random sampling.

Statistical hypotheses are about how randomness affects our data. To decide if the data gives us enough evidence to conclude that drinking brandy changes body temperature we will test a null hypothesis. Null hypotheses are always hypotheses of no difference, or randomness. We can express a null hypothesis about our test of the effect of brandy on core body temperature as:

Null hypothesis: at a population level, average body temperature (μ) for people drinking brandy is 98.6°.

In other words, since we know that body temperature for people who aren't drinking brandy is 98.6°, body temperature should still be at the normal human body temperature of 98.6° if brandy has no effect. If the null hypothesis is true, any difference between our experiment's sample mean and this hypothetical population value is just due to random sampling variation.

We test the null hypothesis, but there is another possibility - brandy may have an actual effect on body temperature. We do not know what the body temperature of people who drink brandy should be, but if brandy affects core temperature it definitely shouldn't be 98.6° anymore. We can thus express this alternative hypothesis as:

Alternative hypothesis: at a population level, average body temperature (μ) is not equal to 98.6° for people drinking brandy.

You can see that a null hypotheses is very specific - it specifies a hypothetical value of the population mean exactly. In contrast, alternative hypotheses are not specific at all, they just say "whatever the population mean might be, it is not equal to the null value".

So far this doesn't actually look any different from the decision rules that we set up before. There is a very important difference, though - the null hypothesis is about the population mean, not about the sample mean. We will use the value of the population mean of 98.6° as the center of a sampling distribution, and will ask if the sample mean of 98.7° that we observed is likely to occur by chance, or unlikely to occur by chance when the null hypothesis is true and brandy has no effect on body temperature. This will account for random sampling, and will allow us to draw a conclusion about our scientific question in a way that properly acknowledges the way that randomness affects our data.

The general procedure that all null hypothesis significance tests follow is:

Formal null hypothesis significance testing

The one-sample t-test

The above set of steps are common to all NHST's, but the details are different depending on the data type and experimental design used. In this body temperature experiment example, we have:

The appropriate null hypothesis significance testing procedure to compare a single sample mean to a specified hypothetical population mean is called a one-sample t-test. The steps in the procedure are as follows:

1. State the null (and the alternative)

The null hypothesis will always be the hypothesis of no effect or randomness, and it will be expressed in terms of a population parameter. If there is no effect of brandy drinking we expect the population mean to equal 98.6°.

To make the null hypothesis as precise and clear as possible we can express it in symbolic form. The symbol for "null hypothesis" is Ho, or "h-naught", with the o representing a subscripted zero. We can write the null hypothesis symbolically as:

Ho: μ = 98.6°

or, equivalently, as:

Ho: μ - 98.6° = 0

This makes it absolutely clear that our null hypothesis is that the mean of the population our data was selected from is 98.6°.

Once the null hypothesis is stated, the alternative hypothesis is just that the null hypothesis is false. Symbolically the alternative hypothesis is:

HA: μ ≠ 98.6°

This statement makes it absolutely clear that if we decide that the null is not true then all our null hypothesis test will tell us is that the population mean is something other than the null value of 98.6°.

2. Calculate a test statistic

The test statistic tells us how different our sample mean is from the null hypothetical value. Mathematically, "difference" implies subtraction, so we could find the difference by subtracting our hypothetical population mean of 98.6° from the sample mean of 98.7°, which gives us 98.7° - 98.6° = 0.1°.

If you recall from our work on confidence intervals, we can use the t-distribution as a mathematical model of randomly sampling means with a given sample size from a population. The advantage of using the t-distribution is that it will allow us to calculate a probability of obtaining a difference of 0.1° from a population with a mean of 98.6° based on the data in just a single sample. But, the units on the x-axis of a t-distribution are standard errors, not degrees Fahrenheit. To use the t-distribution we need to convert the units for our difference into standard errors.

To do this unit conversion we first need to know the standard error for the data set. The standard error for a single sample of data is just the standard deviation divided by the square root of the sample size. Our sample of 20 people had a standard deviation of 0.3, which means that the standard error would be:

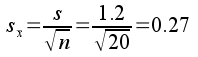
standard error

The units on a standard error are the data units, so there are 0.067° in one standard error for this sample of data.

Now to get our observed t-value test statistic we just need to know how many standard errors 0.1° is. This is just a simple unit conversion, just like converting 120 inches into feet - to make this conversion we would divide 120 inches by the number of inches per foot to get 120/12 = 10 feet. Dividing our observed difference of 0.1 by the number of degrees in a standard error gives us:

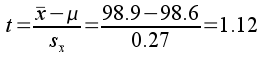
tvalue

This tells us that 98.7° is 1.49 standard errors above 98.6° (to be clear, it's 1.49 standard errors away from 98.6°, and since the value is positive it's above 98.6°). This observed t-value is now in the correct units to compare to a t-distribution to obtain a probability for our experimental result.

3. Compare the test statistic to a sampling distribution to obtain a p-value

To reach our conclusion about the null hypothesis we need to calculate a probability, called a p-value. The p-value is the probability of a very specific thing:

The p-value is the probability of randomly sampling from a population with a mean equal to the null value (μ = 98.6°) and obtaining a sample mean that is at least as different from the null value as the observed sample mean (x̄ - μ = 0.1°).

We will use the t-distribution to obtain the p-value for our observed t-value. Remember from the confidence interval exercise that the t-distribution is a good mathematical model of a sampling distribution for means, and its shape depends on degrees of freedom. For a one-sample t-test degrees of freedom equals the sample size minus 1, which this example is 20-1 = 19.

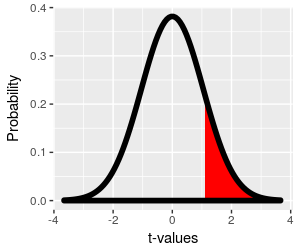
One tailed p-value

The t-distribution with 19 degrees of freedom is shown in the graph to the left.

The probability of getting a sample mean at least t = 1.49 standard errors above 98.6° by chance is the red shaded area from 1.49 to infinity, which is equal to:

p = 0.076

Finding the probability for an observed t-value is best left to the computer - we will use MINITAB to calculate all of our p-values for us.

This p-value is called a one-tailed p-value, because we are only using one tail of the t-distribution to obtain it. We suspect that drinking brandy increases body temperature because it feels like it does, so we may only be interested in the chances that random sampling would produce sample means that are higher than 98.6° - if that's the case then using a one-tailed p-value is appropriate.
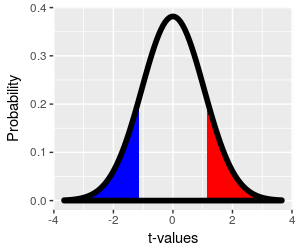
Two-tailed test

However, it's possible that the sensation of warming when we drink brandy is misleading, and that body temperature actually decreases even though we feel warmer. This sort of unexpected result can happen, and we may want to leave open the possibility of the unexpected occurring when we do our work. When we're doing our null hypothesis test we're considering the possibility that our experimental result is only different from 98.6° due to random sampling, and from that perspective the direction of the observed difference isn't important - if it's a randomly generated difference it could just as easily have gone the other way. We account for this possibility by looking at random differences that are just as big as we observed (0.1°, or 1.49 standard errors), but in the opposite direction.

We account for the possibility of unexpected results by using a two-tailed p-value. To include differences as big as we observed in either the positive or negative direction, we would want to include the blue region, which starts at t = -1.49 and extends to negative infinity, as well as the red region, to calculate our p-value.

Since the t-distribution is symmetrical, the area in the blue region is also 0.076, and the two-tailed p-value that uses both the red and blue regions is p = 0.152.

The way to indicate if your p-value is based on one tail or two is in the way you represent the alternative hypothesis. If you are only using the upper tail for the p-value you are only testing for a warming effect, and your alternative hypothesis should be:

HA: μ > 98.6°

If you are testing for an effect of brandy on body temperature, and are interested in finding either an increase or decrease in body temperature, then your alternative hypothesis should be:

HA: μ ≠ 98.6°

We're using the HA: μ ≠ 98.6° alternative, so we would be able to detect either an increase or a decrease in body temperature. Obviously, if you wait to see which direction the difference was and then tested for that direction of difference you would not be conducting a fair, unbiased test. You should always decide whether you're testing for just one direction of change or either direction before looking at your results.

Given this explanation, what should the alternative hypothesis be if you were only interested in testing for a reduction in body temperature from drinking brandy? Click here to see if you're right.

As a general rule, I would recommend using two-tailed tests unless you have a really good reason to use one-tailed tests. It's better to leave open the possibility of an unexpected result. For the brandy experiment, we may think that brandy increases body temperature because drinking it makes you feel warm. But, it is possible that drinking brandy produces that feeling of warmth by moving some of the heat from the core of your body to the surface, which could decrease core body temperature in spite making your skin feel warm. Either possibility would be interesting, and we should use the two-tailed p-value for our test so that either result is detectable.

4. Compare p to α - reject the null hypothesis if p < α, and retain the null hypothesis if p ≥ α

We now have a p-value of 0.152. You can think of this as telling you that if drinking brandy has no effect on core body temperature a difference of 0.1° away from 98.6° would happen 15.2% of the time.

This seems like a pretty high probability of the result being due to random chance, and thus not due to a real effect of brandy, but how do we know that p = 0.152 is big enough to conclude that brandy has no effect?

Unfortunately, the answer is that we can't know for sure, because the only probabilities that indicate certainty are p = 0 (impossible) or p = 1 (definite). Any time we draw a conclusion based on a probability other than 0 or 1 leaves open the possibility that we are wrong. We can't achieve absolute certainty about whether our result is due to random chance or not, but we can decide in advance of conducting the test how low the p-value has to be before we conclude that brandy has an effect. We call this threshold value against which we compare our p-value the alpha level, or simply α.

It's up to the data analyst to set alpha, but even though any value could be used it's traditional to set alpha to 0.05. We draw our conclusion about the null hypothesis using the decision rule:

Our p-value is p = 0.152, greater than 0.05, so we retain the null.

COMMIT THIS DECISION RULE TO MEMORY! This is a very simple rule, but it only works if you remember it!

We already met this decision rule when we were testing normality of data, but in a different form. We "failed" the normality test when p was less than 0.05, and "passed" it when p was greater than 0.05. The AD test of normality is in fact a null hypothesis test, with a null hypothesis that your data are normally distributed. If p is greater than 0.05 you retain this null (and "pass" the test), whereas if p is less than 0.05 you reject this null (and "fail" the test).

By the way, statisticians often prefer to use fail to reject or retain when they talk about the null, rather than accept, because doing so acknowledges that this hypothetical value may still be incorrect, but that our data provides too little evidence against 98.6° as the value of μ to reject it.

5. Draw a scientific conclusion

We retained the null hypothesis that body temperature is equal to 98.6° at the population level. Given this, scientifically speaking we do not have sufficient evidence from our sample mean of 98.7° to conclude that people who drink brandy have a body temperature that is different from 98.6° on average.

If you retain the null hypothesis, you can say your result is not statistically significant. If p had been less than 0.05 we would have rejected the null, and we would have been able to call the difference statistically significant. This phrase can cause mischief, because "significant" and "important" are synonyms in everyday usage, but not in statistics. If you say your results are significant, all you are saying is that your results are unlikely to be due just to random chance, but that isn't the same thing as saying they are biologically important. Biological importance can only be judged based on what you know about the system - if an increase of 0.1 had in fact been statistically significant, would that much increase be enough to use brandy drinking as a way to stay warm? Would such a small increase in body temperature be worth the mental impairment in a survival situation? Such questions aren't addressed by the null hypothesis test - all you learn from the null hypothesis test is whether you're justified in considering your results to indicate a real effect of the treatment you used, or more likely to be due to random chance.

So, now that we understand null hypothesis significance testing, let's return to the logical setup for our experiment. The only change we need to make is in the decision rules, and the changes are in italics:

Now when we assess our results we don't base the decision on whether the sample mean is equal to 98.6°, we base the conclusion on whether the sample mean is significantly different from 98.6°. This change properly accounts for the way that randomness affects our data, and prevents us from interpreting small, random fluctuations as though they indicate real biological effects.

What does it mean to accept the alternative?

When you get a statistically significant result, you reject the null hypothesis and accept the alternative hypothesis. The alternative hypothesis is HA: μ ≠ 98.6°, which just states that the null is wrong. The alternative hypothesis is not that the population mean is equal to the sample mean; that is, definitely not HA: μ = x̄ = 98.7°.

It's important to realize this, because researchers often act as though rejecting the null is evidence that the population mean is equal to the sample mean. This is actually a perfectly sensible thing to do, because when the null is rejected the best estimate we have about the actual value of the population mean is the estimate we get from our sample mean. But bear in mind that the reason for treating 98.7° as the value for μ is because it's the value estimated by x̄. Whether it's at all a good estimate should be evaluated by calculating a confidence interval - a narrow interval around 98.7° would indicate that you have good reason to treat it as the correct value for μ. Understand, though, that the alternative hypothesis doesn't give evidence for any particular value of μ, only against a very specific value of μ, and is therefore by itself not good evidence that μ is equal to the sample mean.

Formal null hypothesis testing - the critical t-value approach

So far, you've learned to compare a p-value to an alpha level to determine whether to reject or retain the null. An alternative approach that you will also see frequently in the scientific literature is to compare the observed t-value to a critical t-value.

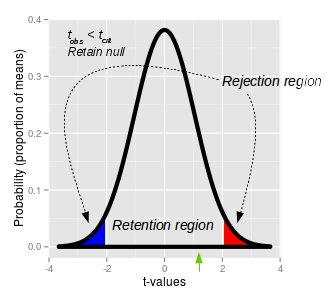
ttest

This graph of a t-distribution illustrates the approach. Once we pick an alpha level of 0.05, we can put 1/2 of it in the upper tail and 1/2 in the lower tail, which defines the upper (red) and lower (blue) rejection regions. The t-values that define the ends of the shaded regions are the critical t-values. The critical t-value for our experiment, with 19 degrees of freedom is tcrit = ±2.1. If an observed t-value falls into either of these rejection regions the probability of observing a t-value of that size is less than 0.05, and we would reject the null.

Between the critical t-values of -2.1 and 2.1 is the retention region. Any t-value that falls within the retention region has a probability of occurring that is greater than 0.05, and would cause us to retain the null.

Our observed t-value of 1.49 (shown by the green arrow below the x-axis) falls inside of the retention region - thus, we retain the null, and conclude there our sample mean of 98.7 is not significantly different from 98.6.

If you click on the picture you'll see that it changes between a p-value approach and a critical t-value approach so you can see how the two methods are related.

α(2): t0.20 t0.10 t0.05
df α(1): t0.10 t0.05 t0.025
1 3.078 6.314 12.706
10 1.372 1.812 2.228
15 1.341 1.753 2.131
16 1.337 1.746 2.120
17 1.333 1.740 2.110
18 1.330 1.734 2.101
19 1.328 1.729 2.093
  

Critical t-values come from t-tables. A portion of a typical t-table is shown here (with some of the degrees of freedom rows removed to make it shorter).

The column labels refer to the alpha level for either two-tailed (α(2)) or one-tailed (α(1)) t-tests. Since we are doing a two-tailed test, we need to use the top row (the α(2) column headings) to pick the column to use - with an alpha level of 0.05 we need to use t0.05.

The row to use is determined by degrees of freedom. With 20 data points is 20-1 = 19, so the critical t-value is in the row labeled with 19 degrees of freedom, and the column labeled with α(2) of t0.05 - the critical t-value is 2.093, which is in red italics.

The graph of rejection and retention regions is a nice way of visualizing how this is working, but we can express all of this with another simple decision rule:

  • If the absolute value of the observed t-value is greater than the critical t-value, reject the null. Observed t-values that are greater than the critical t-value fall into the rejection region of the graph.
  • If the absolute value of the observed t is less than the critical value, retain the null. Observed t-values that are less than the critical t-value fall into the retention region of the graph.

Now you have two methods for doing the same thing, evaluating the null hypothesis, so which should you use?

The good news is that it doesn't matter much. Since the p-value comes from the observed t-value, and the critical t-value comes from the alpha level, both methods are making essentially the same comparison, and the two approach will always lead to the same conclusion about the null hypothesis (assuming you interpret them correctly).

However, we will primarily use the p-value approach in class because it is simple, and because p-values carry some additional information that critical t-values do not - a p-value of 0.00001 is stronger evidence against the null hypothesis than a p-value of 0.049. The critical t-value approach only leads to a "reject/retain" decision, but doesn't give us any information about how strong the evidence supporting our conclusion is, so we will opt for the more informative p-value approach.

Relationship between a one-sample t-test and a confidence interval

If you look at the curve illustrating rejection and retention regions above it should remind you of how we illustrated a confidence interval - it illustrates an interval within which 95% of sample means should be found, if the null is true.

Let's look at how a one-sample t-test compares with a 95% confidence interval for a sample mean, graphically:

Rejection/retention regions in a t-test

95% confidence interval for the sample mean
Rejection region
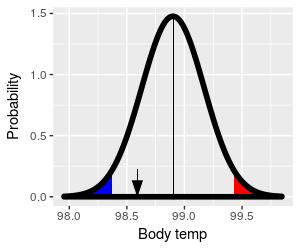 Confidence interval

The retention region is centered on the hypothetical population mean, and it captures 95% of the possible sample means. If you click on the image you can toggle between using t-values as the x-axis and using degrees (remember, calculating t is just a matter of doing a unit conversion to express data units as standard errors, so we can convert back and forth between the data units and t-values without changing the shape of the distribution).

The sample mean 98.7° is the black arrow, and it's within the retention region - we retain the null, and conclude that the population mean is 98.6°.

The sample mean is a sample-based estimate of the population mean. A 95% confidence interval centered on the sample mean of 98.7° uses the t-distribution to find limits that capture 95% of possible sample means. The shaded areas in the tails are the 5% of the possible sample means that are not in the confidence interval. Any mean falling within the confidence interval is considered a possible value for the population parameter.

The hypothetical population mean of 98.6° is shown by the black arrow. It falls inside of the 95% confidence interval, and we would conclude that 98.6° is a possible value for the population mean.

With the graph of a t-test on the left set to show units of degrees, the only difference between the left and right graph is that the left is centered on the hypothetical value of 98.6°, whereas the graph on the right is centered on the sample mean of 98.7°. If we center on the hypothetical population mean, as we do with the t-test, we check if the sample mean falls inside of the interval around the population mean. If we center on the sample mean, as we do with a 95% confidence interval, we check if the hypothetical population mean falls inside of the interval around the sample mean. In both cases we are using sample information to infer the properties of the population the sample comes from.

Why don't we test what we want to know?

Our null hypothesis is that body temperature is equal to 98.6°, but we didn't calculate the probability that the population mean is equal to 98.6°.

Our sample mean is 98.7°, but we didn't calculate the probability that the population mean is equal to 98.7°.

Instead, we assumed that the population mean is 98.6°, and calculated the probability that a random sample from the population would result in a sample mean that is at least 0.1° away from 98.6°. This might strike you as being a little more complicated and indirect than just calculating the probability of the hypothetical value for μ. If so, you are correct - it is, in fact, more complicated and indirect. But there are a couple of reasons we calculate the p-value the way we do.

In contrast, we were able to specify a null hypothetical value for μ exactly, and in advance. This may seem a little odd to you, but it's actually true that null hypotheses are usually easier to specify, because we understand random sampling well enough to predict the average outcome of random sampling exactly. Alternative hypotheses represent what we expect if our experimental treatments are having an effect, and if we had the ability to specify alternative hypotheses exactly we would already know the system so well that hypothesis testing would be unnecessary. We test null hypotheses because we can.

Another advantage people give for null hypothesis testing is that using "no difference" as a default conclusion protects us against confirmation bias, and we need all the help we can get in that regard. For example, since drinking brandy makes us feel warmer, we might be predisposed to believe that it raises body temperature. However, we don't test the hypothesis that drinking brandy makes us warmer - we test the hypothesis that drinking brandy has no effect on body temperature, and only conclude that brandy actually makes us warmer if the mean of our experimental data shows a big enough effect to be statistically significant. This makes it more difficult for us to favor pet hypotheses, and makes it easier for us to objectively evaluate the evidence.

Assumptions of the one-sample t-test

Statistical assumptions are conditions that have to be met in order for a statistical analysis to work correctly. There are two common sources of statistical assumptions: A) general assumptions that ensure that data values that are representative of the population from which they are selected, and B) specific requirements needed by particular test procedures for their p-values to be accurate.

General assumptions (A) are common to essentially all statistical hypothesis tests, regardless of how they obtain their p-values. The two most common ones are:

Independent observations are needed so that the sample size we report is equal to the number of distinct measurements of the population we have. For example, if we selected a single person and measured their body temperature 20 times we would have less information about human body temperature than if we measured the temperatures of 20 different people once each, because repeated measurements of the same person are not independent. Random sampling is needed to ensure that group means are unbiased estimates of the population mean.

An example of a specific assumption for a one-sample t-test (B) is:

We assume that the data are normally distributed, because if this is true the t-distribution is a very accurate model of a sampling distribution for a continuous variable.

The t-distribution is robust to violations of the normality assumption - meaning that the p-values are still accurate if the data are not normally distributed - provided that the non-normality is not too severe, and that the sample size is large. Large sample sizes allow us to rely on the central limit theorem (CLT) - remember, the CLT tells us that the distribution of sample means is bell-shaped for large sample sizes even when the distribution of data is not, and since the t-distribution is a bell-shaped sampling distribution it works well for large sample sizes with any distribution of data. At small sample sizes a skewed or bimodal distribution of data in the population results in a sampling distribution that is not bell-shaped, and the t-distribution is less accurate as a model. Sample sizes of 30 or more are enough to justify using the t-distribution for all but the most severe violations of normality.

We will routinely test for normality before we do t-tests. If we violate normality we will look at the sample size, and if n is 30 or larger we will go ahead and conduct the t-test in spite of the non-normality of our data.

Errors in hypothesis testing

When we reject or retain the null, we are making a definite conclusion based on a probability, which inevitably means that some of our conclusions will be wrong. We can't eliminate errors from statistical hypothesis testing, but we can quantify the chances that we are making one class of mistakes (false positives), and we can take steps to minimize others (false negatives).

The errors we could make depend on the conclusion we draw.

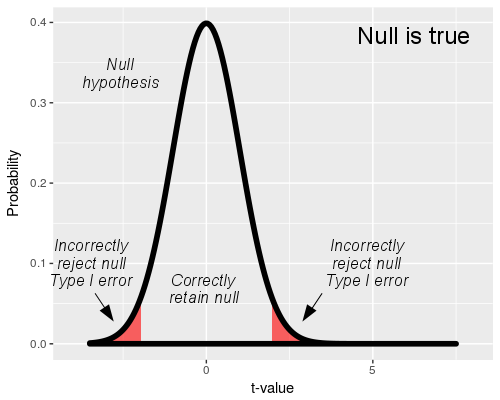
type1

If we reject the null, we are drawing the right conclusion as long as the null is false. If the null is true, rejecting it is a mistake.

We call rejection of a true null a Type I error. Since we think of a rejected null as a positive result, a Type I error is also called a false positive. If we reject the null, the only mistake we could be making is a false positive, Type I error.

We have a lot of control over our Type I error rate - we actually get to specify how big we want it to be. The t-distribution we use in our hypothesis test represents the null hypothesis, so the "Null is true" graph shows a t-distribution with the rejection and retention regions identified. When the null is true, any time a sample mean falls into the rejection region we would reject the null, which would be a mistake.

The rejection region is set by our choice of alpha level. With an alpha level of 0.05 and a true null hypothesis, 5% of sample means will cause us to mistakenly reject the null - thus, the alpha level is our false positive, Type I error rate. Since we set alpha to 0.05 for every test we run, it is always the same regardless of sample size.
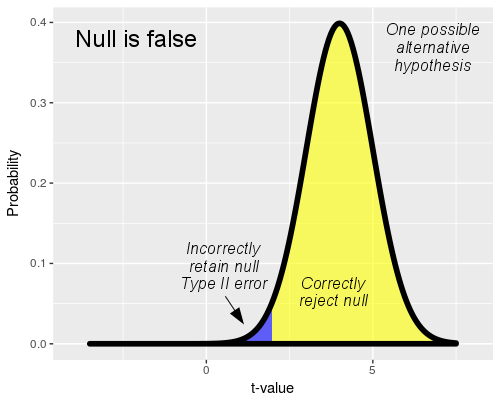
beta and power

If we retain the null we reach the correct conclusion if the null hypothesis is true, but we make a mistake if the null hypothesis is false.

We don't know what the actual population mean is if the null is false, but to illustrate the mistake we can make when we retain the null we need to pick one so that a sampling distribution can be drawn. You'll see that this graph uses a value of t = 4 to represent the alternative, which is equivalent to a population mean that is 4 standard errors above the null value (that is, body temperature of 4 x 0.067 = 0.268 degrees above 98.6°, or μ = 98.868).

When we do a t-test, the rejection and retention regions are defined by the null hypothesis, and are the same here as above. However, if the null is false we are randomly sampling from this alternative distribution instead of the null distribution above. The population mean of μ = 98.868 is far enough away from the null that random samples from this population fall into the rejection region most of the time - the yellow part of the curve represents the sample means that cause us to correctly reject the false null.

However, some of the sample means will be far enough below the population mean of μ = 98.868 that they fall into the retention region. When this happens we retain the null in error. The blue shaded part of the distribution is the portion that falls into the retention region, and represents the rate at which we would fail to reject the false null hypothesis.

Failing to reject a null hypothesis that is false is called a Type II error, which are false negative errors. The blue shaded area under the curve is the probability of a Type II error, which is called beta (β).

The yellow portion of the curve also has a name: statistical power. The yellow part of the curve represents cases in which we were able to detect an actual difference from the null value, and the probability of correctly rejecting a false null is 1-β. We want to be able to detect actual biological effects when they occur, so rejecting a false null is a good thing - we want our experiments to give us good statistical power, like this illustration.

But, there is a problem with calculating Type II error rate and power.

If the null hypothesis is false we don't know what the actual population mean is (if we knew we wouldn't have to do any hypothesis testing!). If we picked a different alternative than this one there would be a different amount of overlap with the retention region, and the Type II error rate (and thus power) would be different. Consequently, if we don't know what the actual population mean is then we can't know what the Type II error rate is either.

So, not only do we not get to specify Type II error rate like we do Type I error rate, we don't even know what the Type II error rate is. What we can do, though, is adopt practices in our experiments that make Type II error rates as low as possible, and thereby increase power, even if we don't know what the rates actually are.

Minimizing false negatives, increasing statistical power

So, how do we make β smaller when we don't know its value? In a general sense, we do this by doing one of two things:

1) make the differences we are trying to detect large, or

2) make the size of the standard error small

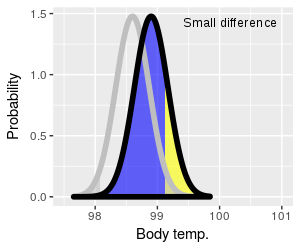Small difference


Let's look first at how the amount of difference between the null value and the actual value of the population mean affects Type II error rate and power. In the graph on the left the t-distribution for the hypothetical value of 98.6° is shown with a thick gray line, and the rejection regions are also shaded in gray. The alternative (which we're assuming now is true) is shown in black. Instead of using t-values for the x-axis these graphs use body temperature to make it more clear what is happening.

You can click on the graph to change it from a small difference to a large difference. The null curve is in the same place for both, but the alternative switches from 98.9° to 99.5° as you switch from small to large difference, respectively.

The blue-shaded region represents false negative (Type II) errors, and the yellow part of the curve is statistical power. When the actual population mean is close to the null value (small difference) most of sample means fall into the retention region - which means that we can expect most of our experimental results will give us Type II errors. Power to detect a small difference is also therefore low (lots of blue, not much yellow).

When the difference is large, most sample means fall into the rejection region - most of our experimental results will give us correct positive test results, so there will be few false negatives and power will be high (little blue, lots of yellow).

So, for a given sample size and standard error, the bigger the difference is that we're trying to detect the greater our power to detect it will be.

In experiments the way we influence the size of difference we are trying to detect is in our choice of the size of the treatment. In our brandy experiment we could increase the difference by having our subjects drink more brandy - if drinking brandy affects core body temperature, then drinking more should cause a bigger change.

However, we don't always have much control over the amount of difference we are trying to detect - it is often a property of the system we study, rather than something we get to set. We also have to be careful about increasing dosages of treatments, because we don't want to overdose the subjects.
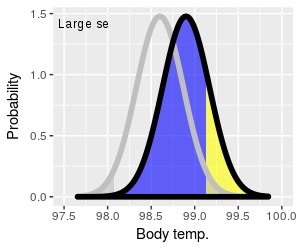
Big se

The other way of increasing power is to decrease the size of the standard error. You can see the effect of reducing standard error by clicking on the graph to the left, which will switch between curves with large standard errors (broad curves) and small ones (narrow curves). Small standard errors increase the amount of yellow (power), and decrease the amount of blue (Type II error).

It's important to note that the alternative curves for both large and small sx̄ have the same mean of 98.9°, so the increase in power isn't due to the size of difference getting bigger. Instead, the increase in power is due to the fact that narrower curves give us more precise estimates of the actual population mean. This is reflected in the graph as a smaller retention region, and a larger retention region, when the standard error is small - the two curves with a small standard error overlap less, and make it more likely that we'll sample a mean that falls into the rejection region, and (correctly) reject the null.

As we learned when we encountered standard errors as components of confidence intervals, there are two ways to reduce the size of a standard error:

Increasing sample size is considered the best way to minimize standard error size, and is always beneficial to the study. It may not always be possible to increase sample sizes for practical reasons (i.e. expense, time constraints, ethical considerations), but bear in mind that using small sample sizes can end up producing such low statistical power that the experiment is not worth doing.

Summing up - statistical errors and power

To summarize, here is a table of the errors you can make depending on whether the null is true or false:


Conclusion drawn
Reality Retain Reject
Null is true No error (1-α) Type I error (α)
False positive
Null is false Type II error (β)
False negative		 No error (power, 1-β)

Bear in mind - you never know if you made an error, because you never know if the null is true or false under real-world experimental conditions. But, if you retain the null the only error you could make is a Type II error, and if you reject the null you could only have made a Type I error.

So, what does brandy do to body temperature?

You may know this already (Mythbusters even did an episode on it), but drinking alcohol does not actually raise your core body temperature. Alcohol causes the capillaries in your skin to dilate (i.e. increase in diameter), which allows more blood to flow from your core to the surface of your body. This makes you feel warm, but by increasing circulation of blood to your body's surface it actually increases heat loss from your core. As long as you aren't in a cold environment that's not a big problem, but for people who already have low core temperatures an increase in heat loss can cause their temperature to drop further, and can cause hypothermia and death.

So, believe it or not, Disney cartoons from the 1930's are not a reliable source of medical information.

Next activity

In this week's activity we will whether our height to stride ratios are equal to 1.19, which is the value used to estimate heights of suspects from stride lengths found at crime scenes.